4.5 Writing Equations of Lines



  1. On August 5, 2010, a gold-and-copper mine collapsed in Chile, trapping 33 miners underground. Rescuers used a drilling rig to reach the miners under the earth’s surface. An escape capsule carried each miner up the shaft at a constant rate as shown in the graph.

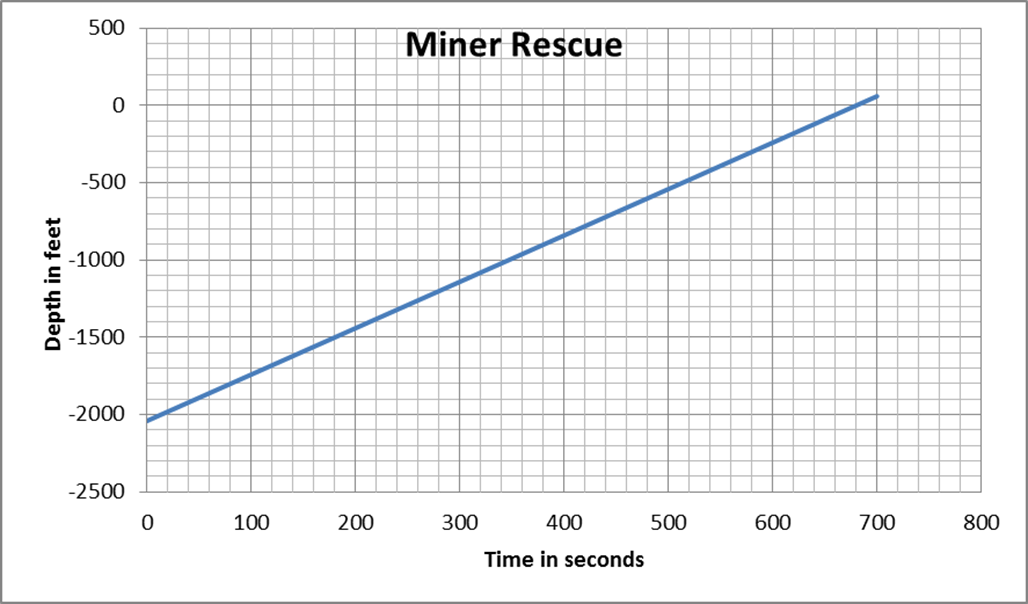
    The Miner Rescue graph is a linear graph that is increasing from left to right. The x-axis represents the time in seconds and goes from 0 to 800 counting by 100. The y-axis represents the depth in feet and goeas from -2500 to 500. Two points on the graph are (0,-2050) and (680,0).

    1. At what underground depth were the miners trapped?

      2. 2040 feet underground

    2. How long has a miner been ascending in the escape capsule when he reaches a depth of 300 feet?

      3. 580 seconds

    3. How long did it take to bring each miner to the surface?

      4. 680 seconds

    4. At what average rate did the escape capsule carry each miner up the shaft?

      5. \( \begin{equation} \frac{-300-0}{580-680}=\frac{-300}{-100}= \text{ 3 feet per second} \end{equation} \)

    5. Write an expression for the depth of the miner during his rescue with respect to time ascending.

      6. y = 3x - 2040

    2. Slope-intercept form of a linear equation:

    y=mx+b where m is the slope and b is the y-intercept.

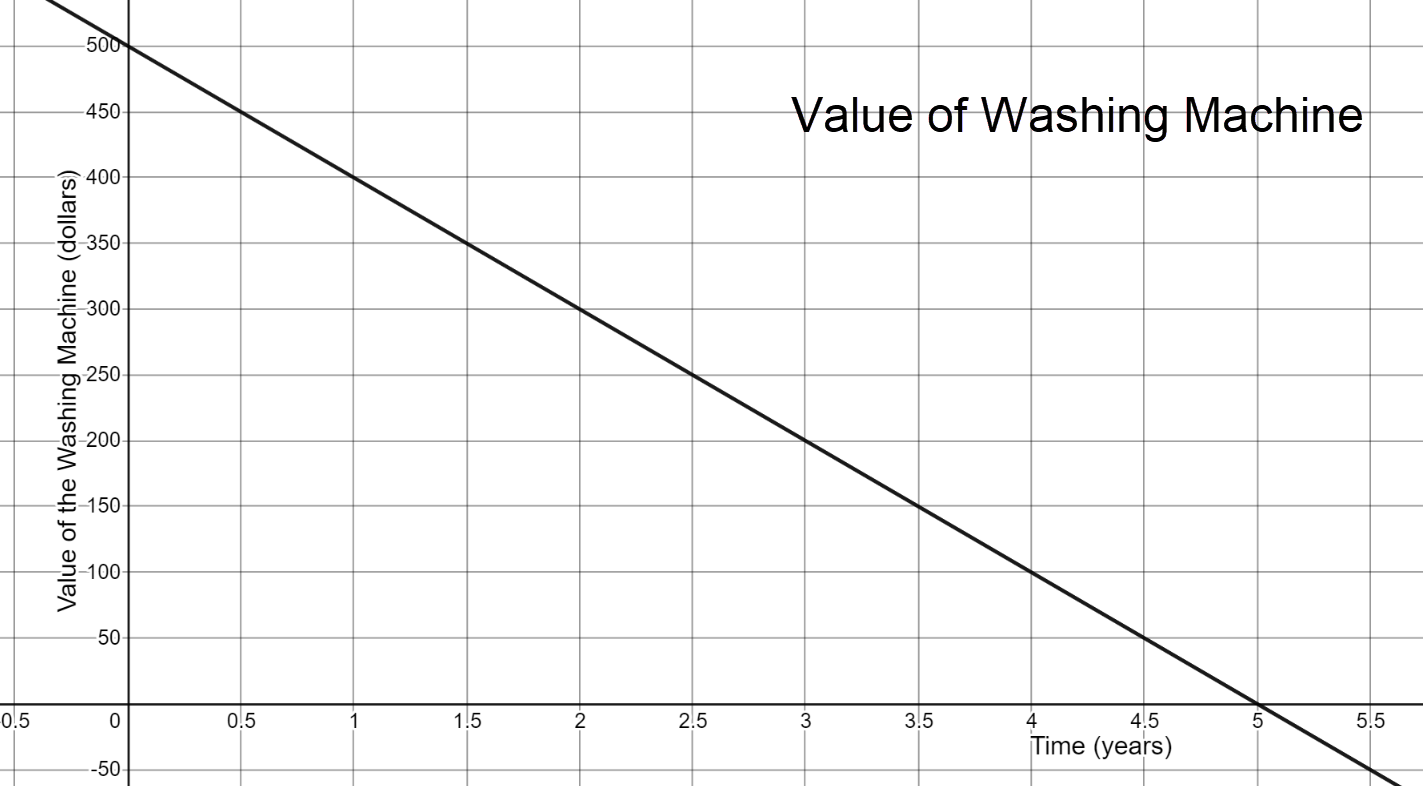
  2. The graph is linear and is decreasing from left to right. The x-axis represents time in years and goes from 0 to 5 counting by 0.5. The y-axis represents the value of a washing machine in dollars and goes from 0 to 500 counting by 50. The two points that are marked on the graph are (0,500) and (5,0).


    Write an equation for the value of the washing machine based on its age.

    y = -100x + 500




  3. The cost of renting a car for one day and driving it 150 miles or less is $54. However the rental company states that if you drive the car 160 miles, they will charge $56.40 , and if you drive the car 185 miles, the charge is $62.40.
    1. How much does the rental company charge for each additional mile over 150 miles?

      \(\frac{62.40-56.40}{185-160}=\frac{6}{25}=$0.24\)

    2. Write an equation for the cost of renting the car for one day based on any extra mileage over 150. Use C for cost and m for extra miles.

      \(C=0.24m+54\)

    3. How much would it cost to rent the car for one day and drive an extra 250 miles?

      \(C=0.24(250)+54=$114\)


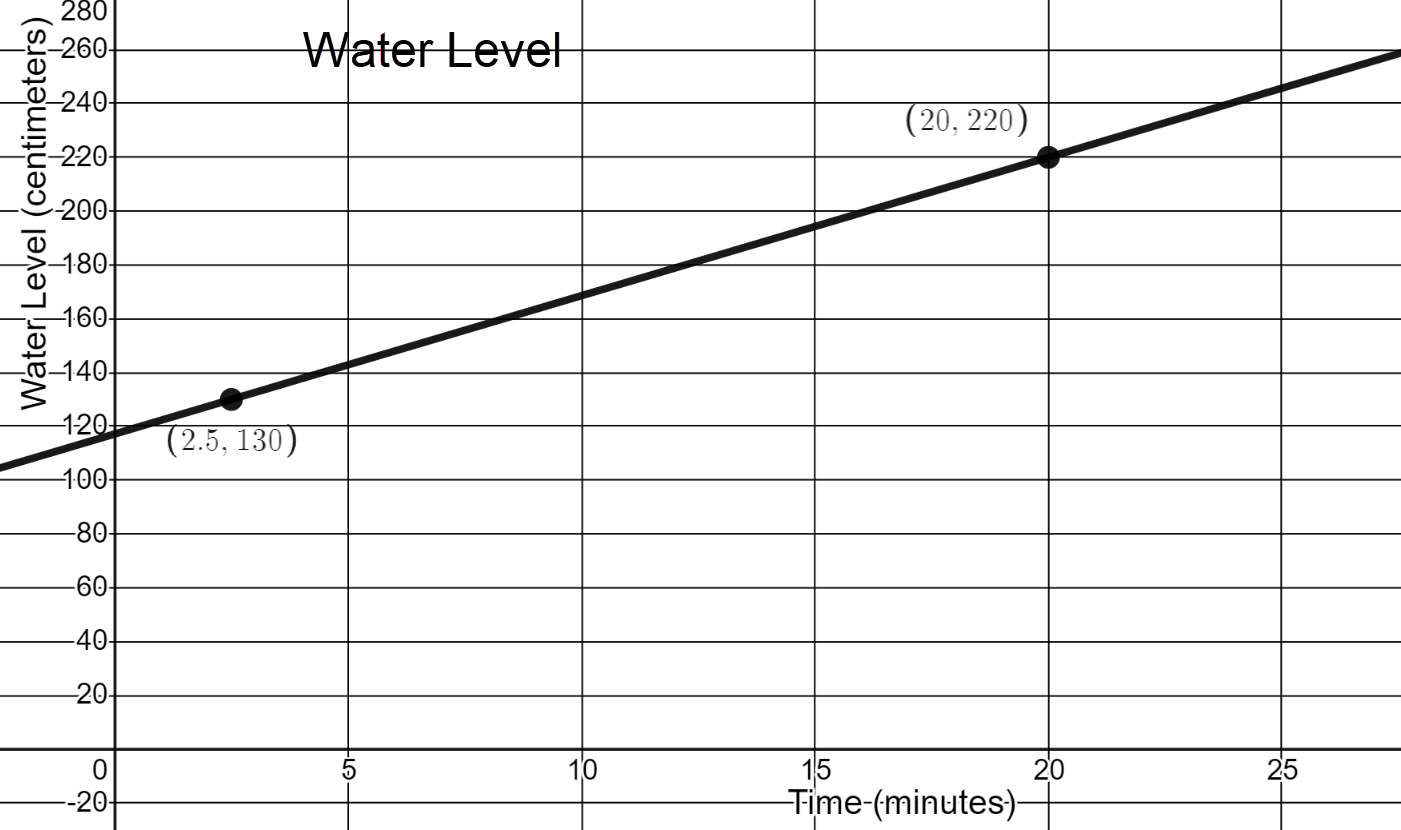
  4. The graph is linear and is increasing from left to right. The x-axis represents time in minutes and goes from 0 to 25 counting by 5. The y-axis represents the water level in centimeters and goes from 0 to 240 counting by 20. The two points that are marked on the graph are (2.5,130) and (20,220).

    1. What is the slope of the line?

      \(\frac{220-130}{20-2.5}=\frac{90}{17.5} \approx 5.14 \text{ cm per minute}\)

    2. What is the initial water level?

      About 117 cm (exactly \(\frac{820}{7}\) cm)

    3. Write an equation for the water level. Use W for water level and t for time in minutes.

      \(W=\frac{36}{7}t+\frac{820}{7}\) or \(W=5.14t-117\)

    4. If the water level keeps increasing at this rate, how high will the water be after 2 hours?

      \(W = 5.14(120) + 117\), so w = 734 cm

  5. You owe money for a hospital bill. The hospital agreed to a payment plan. After paying regularly for 6 months, you still owe $810. After 24 months, you finally paid off the money you owed.
    1. How much did you pay per month on the payment plan?

      \(810/18 = $45\)

    2. How much did you initially owe for the hospital bill?

      \(24(45) = $1080\)

    3. Write an equation for the money owed over time.

      \(y = -45x + 1080 \) or \(y = 1080 – 45x\)