Unit 2 Probability

Review

  1. The General Motors Corporation wants to conduct a test of a new model of Corvette. A pool of 200 drivers has been recruited, 80 of whom are left-handed. When the first person is selected from this pool, what is the probability of not getting a left-handed driver? \(\begin{equation} P(\text { NOT left-handed })=\frac{120}{200}=\frac{3}{5}=0.6 \end{equation}\)
  2. Two psychologists surveyed 478 elementary children in Michigan. They asked students whether their primary goal was to get good grades, to be popular, or to be good at sports. Below is a contingency table giving counts of the students by their goals and demographic setting of their school: rural, suburban, or urban.. Complete the table and answer the questions.
    Grades Most Important Popularity Most Important Sports Most Important Total Number
    Rural 57 50 42

    149
    Suburban 87 42 22

    151
    Urban 103 49 26

    178
    Total Number

    247

    141

    90

    478

    For one randomly selected student, find:

    1. P(Rural) = \(\begin{equation} \frac{149}{478} \approx 0.3117 \end{equation}\)
    2. P(Sports) = \(\begin{equation} \frac{90}{478} \approx 0.1883 \end{equation}\)
    3. P(Suburban and Popularity) = \(\begin{equation} \frac{42}{478} \approx 0.0879 \end{equation}\)
    4. P(Suburban or Popularity) = \(\begin{equation} \frac{250}{478} \approx 0.5230 \end{equation}\)

      P(Suburban) + P(Popularity) - P(Suburban AND Popularity) \(\begin{equation} =\frac{151}{478}+\frac{141}{478}-\frac{42}{478}=\frac{250}{478} \approx 0.5230 \end{equation}\)

    5. P(Popularity | Rural) = \(\frac{50}{149} \approx 0.3356\)
    6. P(Rural | Grades) = \(\frac{57}{247} \approx 0.2308\)

  3. According to cancer.org, there is about a 25% success rate for those who try to stop smoking through medication alone. Find the probability that for 8 randomly selected smokers who use medication, they all successfully quit smoking.

    \((.25)^{8}=0.000015\)

  4. If Knoxville has an annual robbery rate of 0.23%, find the probability that among 3 randomly selected residents, all have been robbed during a given year. (The population of Knoxville is about 183,000.)

    Data from http://www.neighborhoodscout.com/tn/knoxville/crime/

    \((.0023)^{3}=0.000000012\)

  5. Below is a table showing the number of people with various levels of education in 5 countries.
    Post-graduate Some College Some High School Primary or Less No Answer Total Number
    China 7 315 671 506 3 1502
    France 69 388 766 309 7 1539
    India 161 514 622 227 11 1535
    U.K. 58 207 1240 32 20 1557
    USA 84 486 896 87 4 1557
    Total Number 379 1910 4195 1161 45 7690

    If we select someone randomly from the survey, what is the probability the person…

    1. is from the US? \(\frac{1557}{7690}=0.2025\)
    2. had some education but no college? Disjoint

      P(some HS OR Primary or Less) \(=\frac{4195}{7690}+\frac{1161}{7690}-\frac{0}{7690}=\frac{5356}{7690}=0.6965\)

    3. is from France or did some post-graduate study?

      P(France) + P(Post Grad) - P(France AND Post Grad) = \(\frac{1539}{7690}+\frac{379}{7690}-\frac{69}{7690}=\frac{1849}{7690}=.2404\)

  6. Complete the statement: \(P(A)+P(\overline{A})=\) 1
  7. Eye Color: Groups of 5 babies are randomly selected. In each group, the random variable x is the number of babies with green eyes.
    x values Probability P(x)
    0 0.528
    1 0.360
    2 0.098
    3 0.013
    4 0.001
    5 0+
    1. Does it meet the requirement for a probability distribution? Explain

      \(\mathrm{Yes.} \sum P(x)=1 \text { all } P(x) \leq 1 \text{ and } \geq 0\)

    2. Expected Value: E(x) = .599          Mean \(\mu= \) .599
    3. Variance:  \(\sigma^{2}= \) .5262          Standadard Deviation \(\sigma = \) \(\sqrt{.5262}=.7254\)
    4. Minimum Usual Value: -.8518      Maximum Usual Value: 2.049
    5. Would it be unusual to have 0 babies out of 5 randomly selected babies with green eyes?

      No. 0 is between max and min of usual values (-.8518, 2.049)

    6. Would it be unusual to have 2 babies out of 5 randomly selected babies with green eyes?

      No. 2 is between (-.8518, 2.049) . Also, P(x = 2) = .098 is not less than .05.

      7. Find the following probabilities (assuming 5 randomly selected babies)

    7. Probability of exactly 2 green eyed babies: \(P(x=2)=.098\)
    8. Probability of 3 or more green eyed babies: \(P(x \geq 3)=.013+.001+0^{+}=.014\)
    9. Probability of at least 1 green eyed baby: \(P(x \geq 1)=1-P(x=0)=1-.528=.472\)
    10. Probability of at most 1 green eyed babies: \(P(x \leq 1)=P(x=0)+P(x=1)=.528+.360=.888\)
    11. Probability of no more than 1 green eyed babies: \(P(x \leq 1)=.888\)
  8. Find the probability of getting exactly 3 correct responses among 5 different requests from AT&T directory assistance. Assume in general, AT&T is correct 90% of the time.

    n = 5     x = 3     p = 0.9     q = 0.1

    \(P(x)=\frac{5 !}{2 ! 3 !}(0.9)^{3}(0.1)^{2}=0.073\)

  9. Your brother baked a large batch of cookies. He put chocolate chips in 45% of the cookies. He randomly selects 10 cookies to give to a friend. What is the probability that 6 of the cookies contain chocolate chips?

    \(n : 10, p : 0.45 \quad P(x=6)=0.1595678\)

  10. How would you work each of the following problems using Technology?

    60% of the class likes chocolate. If 20 students are randomly selected, find the probability: n = 20      p = 0.60

    Words Probability Statement Calculated Probability Unusual (Yes or No)
    a. 4 like chocolate

    \(P(x=4)\)

    0.0003

    Yes
    b. No more than 5 like chocolate

    \(P(x \leq 5)\)

    0.0016

    Yes
    c. 7 or more like chocolate

    \(P(x \geq 7)\)

    0.9935

    No
    d. More than 7 like chocolate

    \(P(x>7)\)

    0.9790

    No
    e. Less than 13 like chocolate

    \(P(x<13)\)

    0.5841

    No
  11. What is the mean and standard deviation for the probability distribution (of 20 randomly selected students from a class in which 60% of the students like chocolate)?

    Mean: 12      Standard Deviation: 2.2

    12. The Empirical Rule
    1. The average life expectance of a specific brand of tires is 40,000 miles and has a mound shaped distribution (bell-shaped). The standard deviation is 7,500 miles.
      1. Construct and label a bell curve representing the distribution.

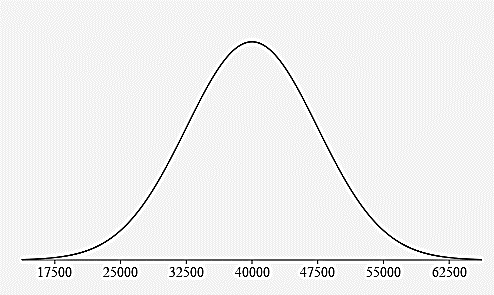
        A normal curve with the mean and 3 standard deviations from the mean labeled on the horizontal axis. They are 17500, 25000, 32500, 40000, 47500, 55000, and 62500.

      2. Estimate the percentage of all tires that have a life expectancy:

        Below 32,500 miles? \(0.15\%+2.35\%+13.5\%=16\%\)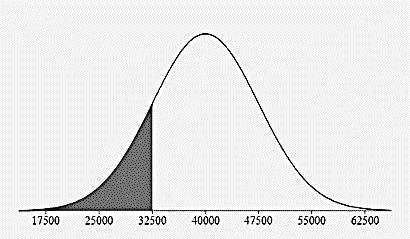

        A normal curve with the mean and 3 standard deviations from the mean labeled on the horizontal axis. They are 17500, 25000, 32500, 40000, 47500, 55000, and 62500. The area under the cirve is shaded to the left of 32500.

        Above 25,000 miles? \(97.5\% = 13.5\% + 34\% + 34\% 13.5\% + 2.35\% + 0.15\%\)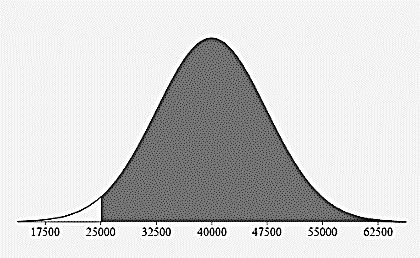

        A normal curve with the mean and 3 standard deviations from the mean labeled on the horizontal axis. They are 17500, 25000, 32500, 40000, 47500, 55000, and 62500. The area under the curve is shaded to the right of 25000

        Between 40,000 and 55,000 miles? \(47.5\%=34\% + 13.5\%\)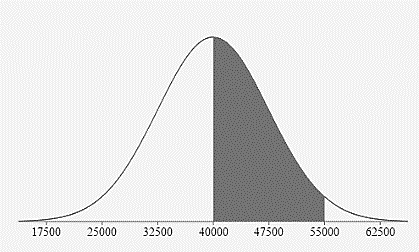

        A normal curve with the mean and 3 standard deviations from the mean labeled on the horizontal axis. They are 17500, 25000, 32500, 40000, 47500, 55000, and 62500. The area under the curve is shaded between 40000 and 55000.

    2. According to dairymoos.com, the mean weight of an adult cow is 1500 lb. Assuming the weights are normally distributed with a standard deviation of 180lb.
      1. Construct and label a bell curve representing the distribution.

        A normal curve with the mean and 3 standard deviations from the mean labeled on the horizontal axis. They are 960, 1140, 1320, 1500, 1680, 1860, and 2040.

      2. Estimate the percentage of adult cows that weigh:

        Between 1320 lbs and 1860 lbs? \(81.5\%=34\% + 34\% + 13.5\%\)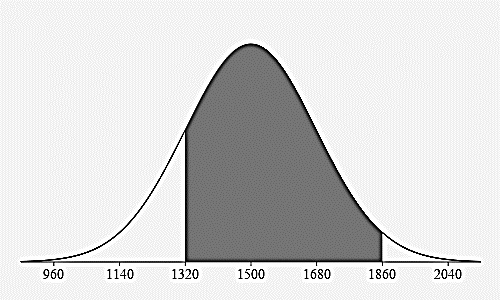

        A normal curve with the mean and 3 standard deviations from the mean labeled on the horizontal axis. They are 960, 1140, 1320, 1500, 1680, 1860, and 2040. The area under the curve is shaded between 1320 and 1860.

        Less than 1500 lbs? \(50\%=0.15\% + 2.35\% + 13.5\% + 34\%\)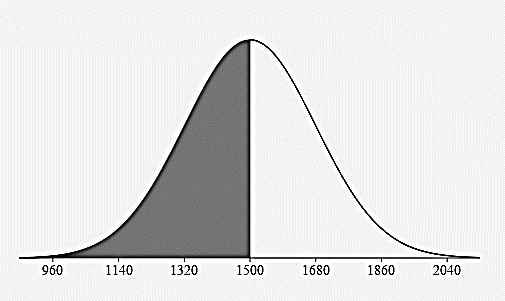

        A normal curve with the mean and 3 standard deviations from the mean labeled on the horizontal axis. They are 960, 1140, 1320, 1500, 1680, 1860, and 2040. The area under the curve is shaded to the left of 1500.

        More than 1680 lbs? \(16\%=13.5\% + 2.35\% + 0.15\%\)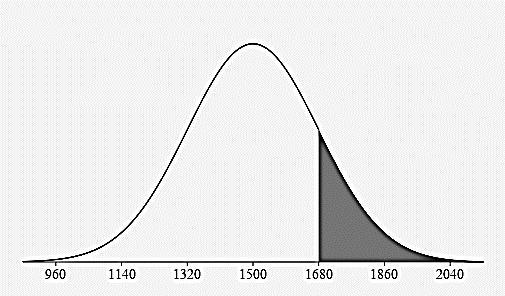

        A normal curve with the mean and 3 standard deviations from the mean labeled on the horizontal axis. They are 960, 1140, 1320, 1500, 1680, 1860, and 2040. The area under the curve is shaded to the right of 1680.

      3. z-Scores
    3. Heights of the members of a high school sport have a bell-shaped distribution with a mean of 161cm and a standard deviation of 7cm.
      1. Find a z score for a team member that is 156 cm tall: \( z_{156}=\frac{156-161}{7}=-0.71\)

        What does this z-score mean in words: The team member’s height of 156 cm is 0.71 standard deviations below the mean of 161 cm.

      2. Find a z score for a team member that is 170 cm tall: \(z_{170}=\frac{170-161}{7}=1.29\)

        What does this z-score mean in words: The team member’s height of 170 cm is 1.29 standard deviations above the mean of 161 cm.

      3. Find a z score for a team member that is 161 cm tall: \(z_{161}=\frac{161-161}{7}=0\)

        What does this z-score mean in words: The team member’s height of 161 cm is 0 standard deviations above or below the mean of 161 cm.