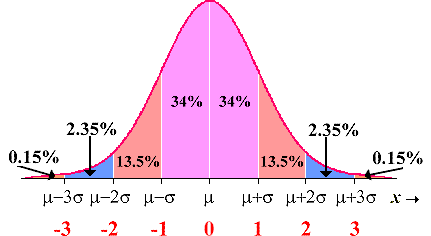
2.5 Empirical Rule

Calculating z-scores


What is a z-score?

the number of standard deviations a given value of x is above or below the mean.

What is the formula for calculating the z-score within a normally distributed population?

\(Z=\frac{x-\mu}{\sigma}\)
  1. Compare the following z-scores and interpret the results. The mean ACT score at Lincoln High School is 24 with a standard deviation of 4. The mean SAT score is 1100 with a standard deviation of 80. If Alice scores 32 on the ACT and Bob scores 1200 on the SAT, which has a better score, relative to the sample data?
    1. Alice's score on the ACT
      1. Alice's z-score:

        \(\mu=24 ; \quad \sigma=4 ;\quad x=32 ;\quad Z=\frac{x-\mu}{\sigma}\)

        \(Z_{32}=\frac{32-24}{4}=2.00\)

      2. What does this z score mean (in words)?

        Alice’s ACT score of 32 is 2 standard.deviations above the population mean of 24.

      3. Sketch a bell curve and mark the score on the curve

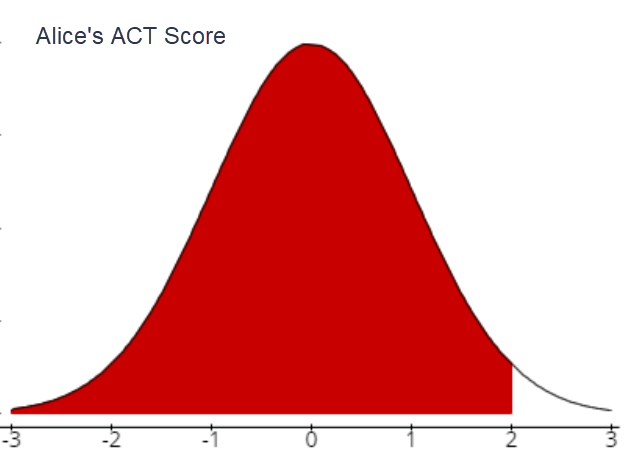
        A bell curve with a mean of 0. Three standard deviations above and below the mean are also marked Alice's z-score of 2 is marked with a the area below shaded in red under the curve.

    2. Bob's score on the SAT
      1. Bob's z-score:

        \(\mu=1100 ; \quad \sigma=80 ; \quad x=1200\)

        \(Z_{1200}=\frac{1200-1100}{80}=1.25\)

      2. What does this z score mean (in words)?

        Bob’s SAT score of 1200 is 1.25 standard deviations above the population mean of 1100.

      3. Sketch a bell curve and mark the score on the curve

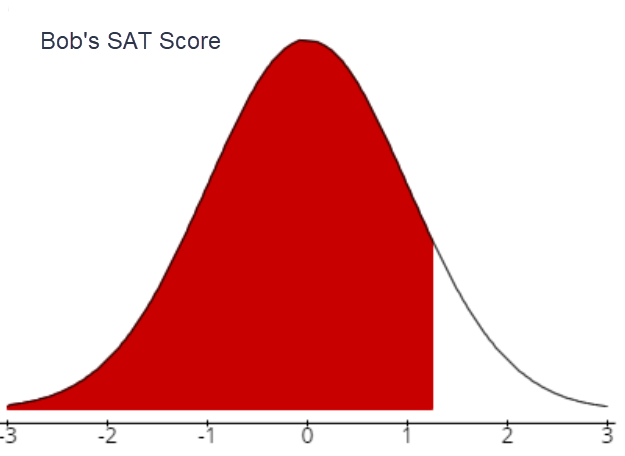
        A bell curve with a mean of 0. Three standard deviations above and below the mean are also marked Bob's z-score of 1.25 is marked with a vertical line that is 1.25 standard deviations above the mean and the area under the curve is shaded red below 1.25.

    3. Relative to other students in the population, which score is better?

      Alice’s relative score is better. She is 2 standard deviations above the mean. Bob’s score is only 1.25 standard deviations above the mean.

    2. The Empirical Rule for Bell Shaped Distributions

    In a bell-shaped distribution of data:


    What percent of the values fall within 1 standard deviation of the mean? 68%


    What percent of the values fall within 2 standard deviations of the mean? 95%


    What percent of the values fall within 3 standard deviations of the mean? 99.7%


    Label the percentages on the bell-shaped distribution:


    A picture of a bell shaped curve. The mean is at the highest point of the curve, the top of the bell with 0 labeled underneath. Three standard deviations below the mean are marked to the left with -3, -2, -1 and three standard deviations above the mean are marked to the right with 1, 2, 3.

    A picture of a bell shaped curve. The mean is at the highest point of the curve, the top of the bell. 34% of the area under the curve is one standard deviation to the left of the mean and one standard deviation to the right of the mean. One standard deviation to the left of the mean is labeled mu minus sigma. One standard deviation to the right of the mean is labeled mu plus sigma. 13.5% of the area under the curve is between one standard deviation and two standard deviations to the left of the mean and to the right of the mean. Two standard deviations are labeled mu minus two times sigma and mu plus two times sigma. 2.35% of the area under the curve is between two standard deviations and three standard deviations to the left of the mean and to the right of the mean. Three standard deviations from the mean are labeled mu minus three times sigma and mu plus three times sigma. 0.15% of the area under the curve is more than three standard deviations from the mean. Usual data is between two standard deviations to the left of the mean and two standard deviations to the right of the mean. Unusual data is more than two standard deviations from the mean.

  2. IQ SCORES: IQ scores have a bell-shaped distribution with a mean of 100 (\(\mu = 100\)) and a standard deviation of 15 (\(\sigma = 15\)). What percentage of IQ scores are:
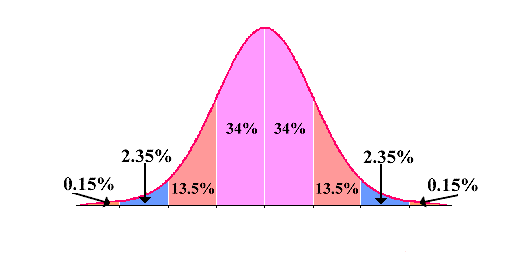
    A picture of a bell shaped curve. The mean is at the highest point of the curve, the top of the bell. 34% of the area under the curve is one standard deviation to the left of the mean and one standard deviation to the right of the mean. 13.5% of the area under the curve is between one standard deviation and two standard deviations to the left of the mean and to the right of the mean. 2.35% of the area under the curve is between two standard deviations and three standard deviations to the left of the mean and to the right of the mean. 0.15% of the area under the curve is more than three standard deviations from the mean.
    1. Between 70 and 130? \(13.5+34+34+13.5=95 \%\)
    2. Below 115? \(0.15+2.35+13.5+34+34=84 \%\)
    3. Above 70? \(13.5+34+34+13.5+2.35+0.15=97.5 \%\)
    4. Between 85 and 130? \(34+34+13.5=81.5 \%\)
    5. Below 145? \(0.15+2.35+1.35+34+34+13.5+2.35=99.85 \%\)
    6. Usual Values are between        and       . \(70 \text { and } 130\)
    7. Unusual Values are below        or above       . \(70 \text { and } 130\)

      8. An unusual event has less than a 5% chance of occurring. Events that fall more than two standard deviations away from the mean are considered unusual.

      Give the formulas for the following:

      Mimimum usual value:

      \(\mu-2 \sigma=100-2(15)=70\)

      Maximum usual value:

      \(\mu+2 \sigma=100+2(15)=130\)

  3. Sketchy Milk Company: A dairy fills gallons of milk with a mean of 125.0 fluid ounces and a standard deviation of 0.3 fluid ounces. The volumes have a bell-shaped distribution. Using the empirical rule, what is the approximate percentage of milk amounts: A picture of a bell shaped curve. The mean is at the highest point of the curve, the top of the bell. 34% of the area under the curve is one standard deviation to the left of the mean and one standard deviation to the right of the mean. 13.5% of the area under the curve is between one standard deviation and two standard deviations to the left of the mean and to the right of the mean. 2.35% of the area under the curve is between two standard deviations and three standard deviations to the left of the mean and to the right of the mean. 0.15% of the area under the curve is more than three standard deviations from the mean.

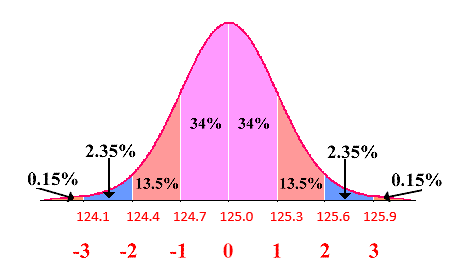
    A picture of a bell shaped curve. The mean is at the highest point of the curve, the top of the bell. The mean is 125.0. 34% of the area under the curve is one standard deviation to the left of the mean and one standard deviation to the right of the mean. One standard deviation to the left of the mean is 124.7. One standard deviation to the right of the mean is 125.3. 13.5% of the area under the curve is between one standard deviation and two standard deviations to the left of the mean and to the right of the mean. Two standard deviations to the left of the mean is 124.4 and two standard deviations to the right of the mean is 125.6. 2.35% of the area under the curve is between two standard deviations and three standard deviations to the left of the mean and to the right of the mean. Three standard deviations to the left of the mean is 124.1 and three standard deviations to the right of the mean is 125.9. 0.15% of the area under the curve is more than three standard deviations from the mean.

    1. Between 124.4 fluid ounces and 125.6 fluid ounces? \(13.5+34+34+13.5=95 \%\)
    2. Below 124.7 fluid ounces? \(0.15+2.35+13.5=16 \%\)
    3. Above 124.7 fluid ounces? \(34+34+13.5+2.35+0.15=84 \%\)
    4. Between 125.0 fluid ounces and 125.9 fluid ounces? \(34+13.5+2.35=49.85 \%\)
    5. Usual values are between        and       ? \(124.4 \text { and } 125.6\)

      Minimum usual value: \(\mu-2 \sigma=125.0-2(0.3)=124.4\) fluid ounces

      Maximum usual value: \(\mu+2 \sigma=125.0+2(0.3)=125.6\) fluid ounces

    6. Unusual Values are below        or above       . \(124.4 \text { and } 125.6\)

  4. Giraffes have a mean height of 18 feet with a standard deviation of 0.8 feet. African elephants have a mean height of 10.6 feet with a standard deviation of 1.2 feet.
    1. Calculate the z-score for a giraffe that is 15 feet tall.

      \(z=\frac{15-18}{0.8}=-3.75\)

    2. What does this z-score tell you about the height of a 15-foot giraffe?

      It is unusually short. The height is 3.75 standard deviations below the mean.

    3. Calculate the z-score for an elephant that is 15 feet tall.

      \(z=\frac{15-10.6}{1.2}=3.67\)

    4. What does this z-score tell you about the height of a 15-foot elephant?

      It is unusually tall. The height is 3.67 standard deviations above the mean.

    5. Calculate the height of a giraffe whose height is 2.3 standard deviations above the mean.

      \(x=18+(2.3)(0.8)=19.84\)  feet

    6. Calculate the height of an elephant whose height has a z-score of -1.6.

      \(x=10.6+(-1.6)(1.2)=8.68\)  feet

    7. Is a 16.5-foot tall giraffe considered unusual?

      No. The minimum usual value is 18 - 2(0.8) = 16.4 feet.

    8. What is the range for usual heights of African elephants?

      8.2 feet to 13 feet