1.2 Graphing Data


Point A is graphed on the number line below. The scale of the number line is 2 since the scale marks are 2 units apart.

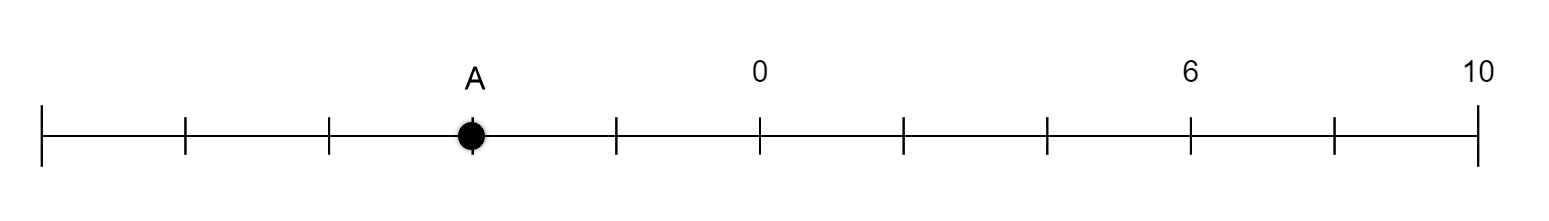
A number line with 0 labeled in the middle, 6 labeled 3 scale marks to the left of 0, and 10 labeled 5 scale marks to the left of 0. Point A is graphed 2 scale marks to the left of 0. There are a total of 11 scale marks on the number line.

Number Lines

Determine the scale of each number line. Label EVERY scale mark. Graph each point with a big dot at the appropriate location and label the point.

  1. A = 2
    B = 12
    C = 7.5

    A number line with 0 labeled on the left end, 4 labeled 4 units to the right, and 9 labeled 5 units further to the right. There are a total of 13 scale marks on the number line.

    Point A=2 is graphed at two scale marks to the right of 0. Point C=7.5 is seven and a half scale marks to the right of 0. Point B=12 is twelve scale marks to the right of 0.

  2. A = 250
    B = 100
    C = 0

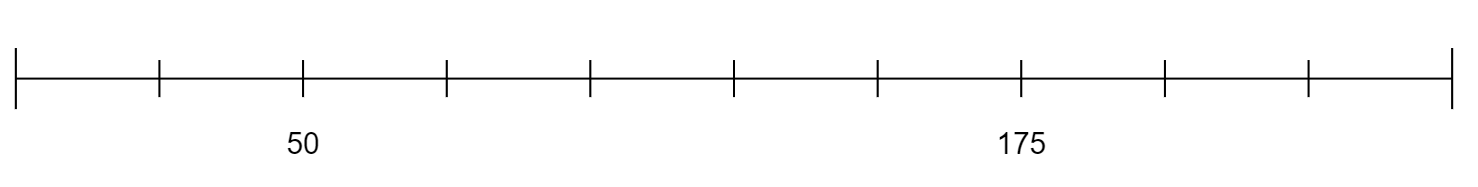
    A number line numbered with 50 marked 2 scale marks in from the left and 175 marked 5 scale marks to the left of 50..

    A number line starting at 0 and going to 250 with 20 scale marks, each representing 25 units. Point C is marked at 0, the first scale mark on the left side of the graph. Point B is marked at 100, four marks after the 0. Point A is marked at 250 the farthest right scale mark.

  3. A = 40
    B = -30
    C = 85

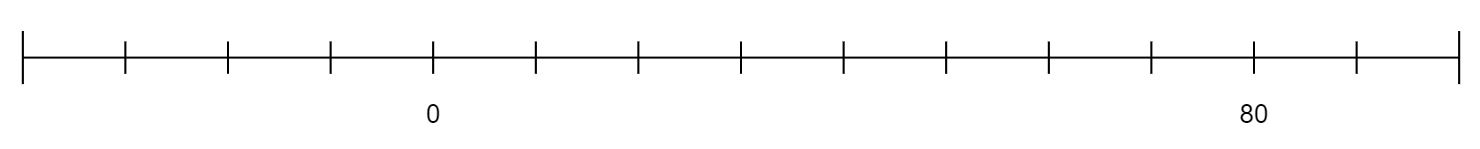
    A number line with 0 on the 4th scale mark from the left and 80 at the 8th scale mark to the right of 0.

    A number line that start at -40 and goes to 100 with each scale mark representing 10 units. Point B is marked at -30 which is one mark from the left side of the number line. Point A is marked at 40, which is 7 marks to the right of Point B. Point C is marked at 85, which is 5 1/2 marks to the right of Point A.

  4. A = 3.5
    B = 0.5
    C =-6

    A number line with 24 scale marks. 2 is graphed 18 marks from the left. 3 is graphed 2 marks after 2. 4 is graphed 2 marks after 3, and 5 is marked 2 marks after 4.

    A number linethat starts at -7 and goes to 5 with each scale mark representing 0.5 units. Point C is graphed at -6, which is 2 marks from the left end of the number line. Point B is graphed at 0.5 which is 15 marks from the left end of the number line. Point A is graphed at 3.5, which is 21 marks from the left end of the number line.

  5. A = 6.8
    B = 6.4
    C = 5.2

    A number line with 5 as the starting number, 6 labeled 5 scale marks to the right of 5, and 7 labeled 5 scale marks to the right of 6..

    Point C is graphed at 5.2, which is one scale mark to the right of 5. Point B is graphed at 6.4, which is two scale marks to the right of 6. Point A is graphed at 6.8, which is 4 scale marks to the right of 6.

    6.  

    Graphing Points

    Point G is located at the ordered pair (-2,4)


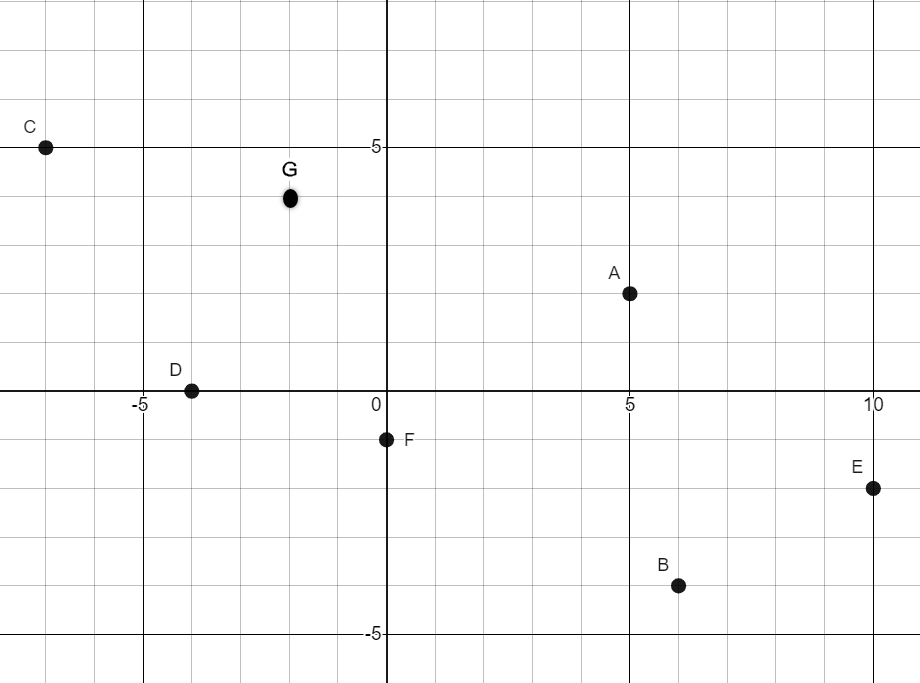  6. Coordinate plane graph with six points graphed. Point A is five units to the right of the origin and up two units. Point B is six units to the right of the origin and down four units. Point C is seven units to the left of the origin and up five units. Point D is four units to the left of the origin. Point E is ten units to the right of the origin and down two units. Point F is one unit down from the origin.

    Write the ordered pair for each point on the graph.
    • Point A

      • (5,2)

    • Point B

      • (6,-4)

    • Point C

      • (-7,5)

    • Point D

      • (-4,0)

    • Point E

      • (10,-2)

    • Point F

      • (0,-1)

    • Draw a line passing through points D and F

      • Line is decreasing from left to right. Line passes through points (-4,0) and (0,-1).

    • Name the y-intercept of this line.

      • Point F (0,-1)

    • Name the x-intercept of this line.

      • Point D (-4,0)

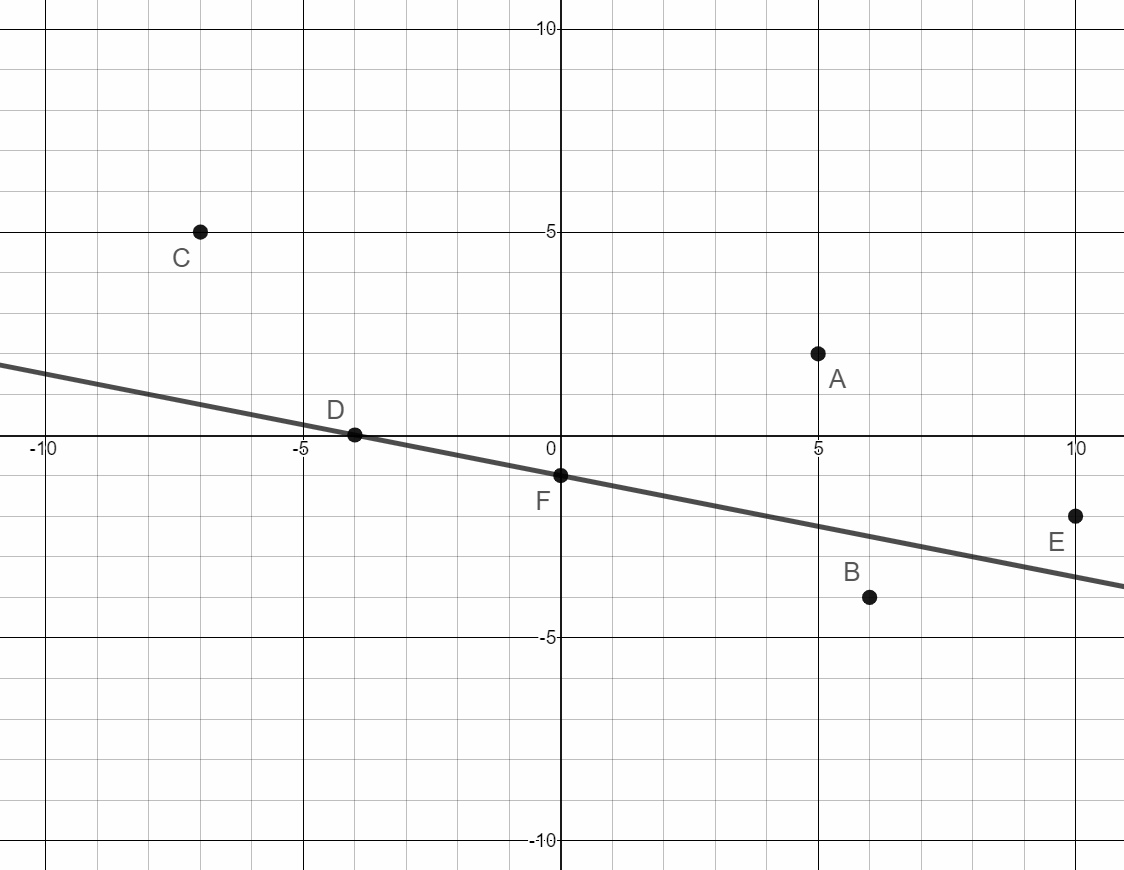
    7. Frequency Distributions

    • Classes or Bins are intervals of equal width used to sort data.
    • Lower Class Limits are the smallest numbers that can actually belong to a class.
    • Upper Class Limits are the largest numbers that can actually belong to a class.
    • Class Midpoints are the values in the middle of a class.
    • Class Width is the difference between two consecutive Lower Class Limits.

  7. The following frequency distribution shows the ages of students in an evening section of Statistics at Pellissippi. Use the frequency distribution to construct a relative frequency distribution.
    Age of PSCC Stat Students Frequency Relative Frequency Relative Frequency
    (in percents)
    16-25 3

    \(\frac{3}{32}=0.094\)

    9.4%
    26-35 7

    \(\frac{7}{32}=0.219\)

    21.9%
    36 - 45 12

    \(\frac{12}{32}=0.375\)

    37.5%
    46 - 55 8

    \(\frac{8}{32}=0.25\)

    25%
    56 - 65 2

    \(\frac{2}{32}=0.063\)

    6.3%

    \(\sum f=32\)

    1.001

    100.1%

  8. What is the upper class limit of the 3rd class? 45
  9. What is the lower class limit of the 5th class? 56
  10. What is the class width? 10
  11. What is the midpoint of the 1st class? 20.5

    12. Cumulative Frequency Distributions (Totals)

  12. Use the given frequency distribution to construct a cumulative frequency distribution.
    • Each class is defined as: less than the lower class limit of the next class
    • Add all frequencies of the current class and all previous classes. This is the cumulative frequency.

    Age Range Frequency Cumulative Age Ranges Cumulative Frequency
    16 - 25 3 Less than 26

    3
    26 - 35 7

    Less than 36

    10
    36 - 45 12

    Less than 46

    22
    46 - 55 8

    Less than 56

    30
    56 - 65 2

    Less than 66

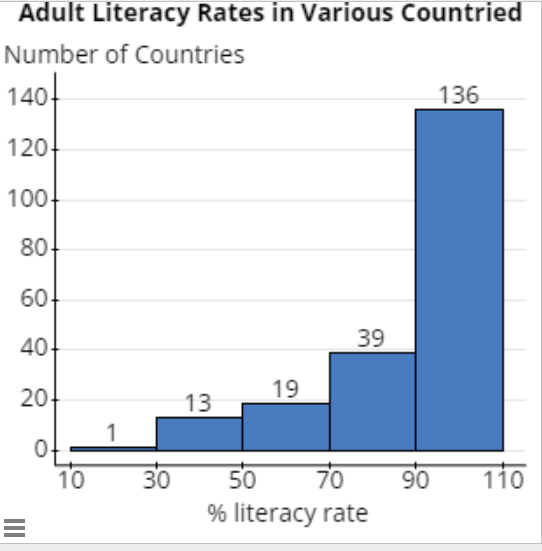
    32

  13. Literacy Rates: Load the Literacy Rates World data set in StatCrunch. The data represent the adult literacy rates for various countries. Adult literacy rate is the percentage of people ages 15 and above who can, with understanding, read and write a short, simple statement in their everyday life. Source: World Population Review Literacy Rates

    Create a Frequency Distribution and Histogram for the data. Determine the class width if you want to create a table with 5 classes.

    The minimum value from the data is: 19.1%

    The maximum value from the data is: 100%

    Calculate the class width using the minimum data value, maximum data value, and number of classes:

    \(\frac{100-19.1}{5}=\frac{80.9}{5}=16.18\)

    When calculating class width, always round up to the next value. Because we calculated 16.18, we will use a class width of 20. For our frequency distribution, we will have a more usable frequency distribution if we set 10 as our lower class limit instead of 19.1.

    Literacy Rate Frequency
    10.0 – 29.9

    1

    30.0 – 49.9

    13

    50.0 – 69.9

    19

    70.0 – 89.9

    39

    90.0 – 109.9

    136

    A histogram representing the adult literacy rates in various countries. The horizontal axis represents the literacy rates in percentages. The vertical axis represents the number of countries in whose literacy rate corresponds to one of the 5 ranges and goes from 10 to 110, counting by 20. Each bar represents the same ranges as the ones described in the table, 10-29.9, 30-49.9, 50-69.9, 70-89.9, and 90-109.9. The height of the bars is determined by the number of countries that are represented in the ranges, 1, 13, 19, 39, and 136 respectively.

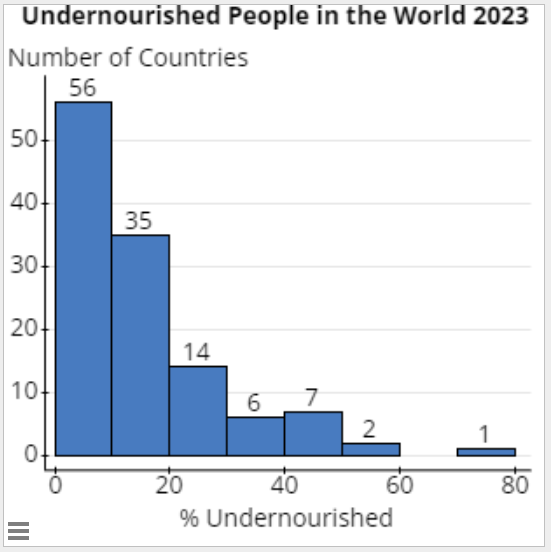
  14. Malnutrition – Percent of undernourished population: Load the Undernourished data set in StatCrunch. The data represent the percentage of each country's population that is undernourished. The prevalence of undernourishment is the share of people who do not get enough calories to live a healthy life.

    Source: Worldometer Undernourished Data


    Create a Frequency Distribution and Histogram for the data. The frequency distribution should have 8 classes.

    Midpoint % undernourished Frequency

    4.95

    		 0.0- 9.9

    56

    14.95

    10.0-19.9

    35

    24.95

    20.0-29.9

    14

    34.95

    30.0-39.9

    6

    44.95

    40.0-49.9

    7

    54.95

    50.0-59.9

    2

    64.95

    60.0-69.9

    0

    74.95

    70.0-79.9

    1

    A histogram representing undernourished people in 2023. The horizontal axis represents the percent of undernourished and the ranges are 0-9.9, 10-19.9, 20-29.9, 30-39.9, 40-49.9, 50-59.9, 60-69.9, and 70-79.9. The vertical axis represents the number of countries and goes from 0-60 counting by 10. The height of each bar represents the number of countries whose percentage of undernourished falls within the range depicted, 56, 35, 14, 6, 7, 2, 0, and 1 respectively.

    15. Stem-and-Leaf Plots


  15. The following stem and leaf plot gives the fuel economy information (combined city/highway miles per gallon) for Toyota’s 2024 vehicle line. Key 3|5 = 35 miles per gallon
    Stem Leaves
    12 7 7
    11 4 9
    10 4
    9 4
    8
    7
    6
    5 0 2 2 4 7
    4 1 2 6 8 9
    3 0 0 0 0 1 2 2 3 4 4 5 5 5 5 6 6 6 9 9
    2 0 0 1 1 2 2 2 3 3 3 4 4 4 5 5 6 6 6 7 7 8 9 9
    1 7 7 9
    1. What is the lowest miles per gallon for any Toyota vehicle? 17 mpg
    2. What is the highest miles per gallon for any Toyota vehicle? 127 mpg
    3. How many Toyota vehicles have a fuel economy between 30 and 40 miles per gallon, inclusive? 19 vehicles

     

  16. The 400-meter race times for the Class AAA high school athletes who scored in the 2023 TSSAA track and field Tennessee state championship meet are recorded in the following stem and leaf plot. Key 49|1 = 49.1 seconds
    Stem Leaves
    47 1 9
    48 6 7 8
    49 1 3 5
    50
    51
    52
    53
    54
    55
    56 0
    57 0 2 2 4 5 8
    58 3
    1. What was the fastest 400-meter time? 47.1 seconds
    2. How many athletes ran the 400-meter race in under 1 minute? 16
    3. Why is there a gap between 50 and 55 seconds in the data set? No runner ran took between 50 and 55 seconds to run the race.

    17.  

  17. Answer the questions about the Stem-and-Leaf diagram below.

    A Stem-and-Leaf diagram titled Employee Salaries. The stems on the left side are listed vertically and are numbered 4, 5, 6, 7, 8, & 9. The leaves with the 4 are 1, with the 5 are 2, 7, & 8, with the 6 are 5 & 6, with the 7 are 0, 5, 8, 8, & 8, with the 8 are 0 & 0, and finally with the 9 is 5. The key is 5|2 = 52,000.

  18. What is the highest employee salary? $95,000
  19. How many employees salaries are given in the diagram? 14
  20. How many employees earn a $78,000 salary? 3 employees