1.5 Measures of Relative Standing


The World's Highest-Paid Athletes 2023

Open the data set in Stat Crunch “World’s Highest Paid Athletes 2023”:

Source Sportico

  1. Identify the following statistical measures for Total Earnings:
    1. Mean: $112.39 M
    2. Standard Deviation: $54.96 M
    3. Mode: No mode
    4. Minimum: $70 M
    5. Lower Quartile (Q1): $77.7 M
    6. Median: $87.65 M
    7. Upper Quartile (Q3): $125.35 M
    8. Max: $275 M
    9. Range: $205 M
  2. Label the Quartiles on the box plot for Total Pay:

    The title of the box plot is Total Earnings. The x-axis on the box plot is numbered from 60 to 280 and counting by 20 and is labeled Millions of Dollars.

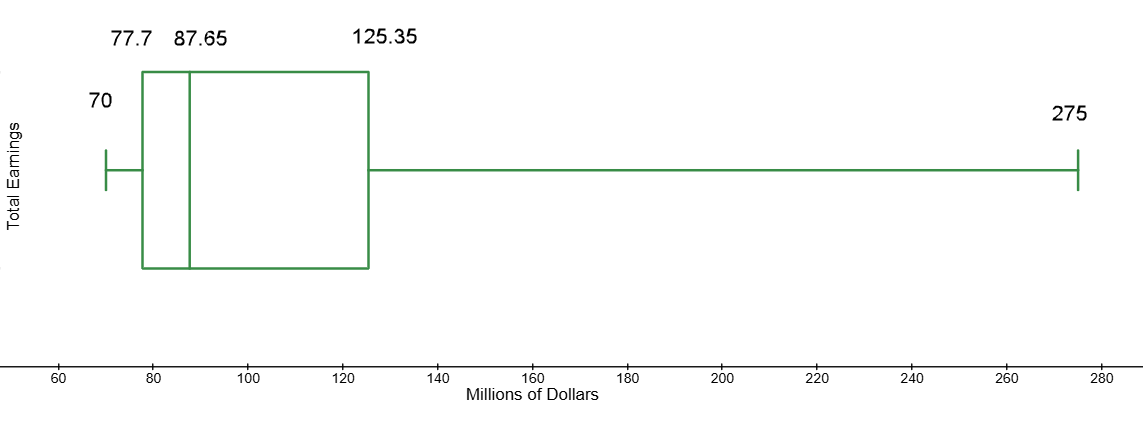
    The title of the box plot is Total Earnings. The x-axis on the box plot is numbered from 60 to 280, counting by 20, and labeled Millions of Dollars. The left whisker is at 70, the minimum number, and the right whisker is at 275, the maximum number. The box that is drawn contains the lower quartile at 77.7, the median at 87.65 and the upper quartile at 125.35.

  3. Determine the Inter-Quartile Range (IQR) for Total Earnings: $47.65 M

    The range of the “middle” 50% of the data is called the interquartile range.

    A chart showing the percent of data in each quartile. There are four equal-size areas of 25% each. The first quartile goes from the minimum data value to Q1. The second quartile goes from Q1 to the median data value, the third quartile goes from the median to Q3, and the fourth quartile goes from Q3 to the maximum data value. The Inter-Quartile Range (IQR) is shaded on the graph between Q1 and Q3, which is the IQR.
  4. How many of the world’s sixteen highest paid athletes for 2023 earned a total pay greater than $125.35 million? 4
  5. How many of the world’s sixteen highest paid athletes for 2023 earned a total pay less than $7.7 million? 4
  6. How many of the world’s sixteen highest paid athletes for 2023 earned a total pay between $90 million and $95 million? 4
  7. How many of the world's sixteen highest paid athletes for 2023 had total earnings the same or lower than the 50th percentile? 8
  8. Lamar Jackson's total earnings is the 31st percentile for the world’s sixteen highest paid athletes for 2023. What does this mean? He earns higher than 31% of the highest paid athletes of 2023.
  9. Use Stat Crunch to compare box plots for Salary/Winnings and Endorsements.
    1. Which data set has a higher median? Salary/Winnings
    2. Which data set has a greater range? Salary/Winnings
    3. In which data set do 50% of the athletes earn between $23.5 million and $55 million? Endorsements
    4. Which data set has more athletes earning less than $40 million? Endorsements

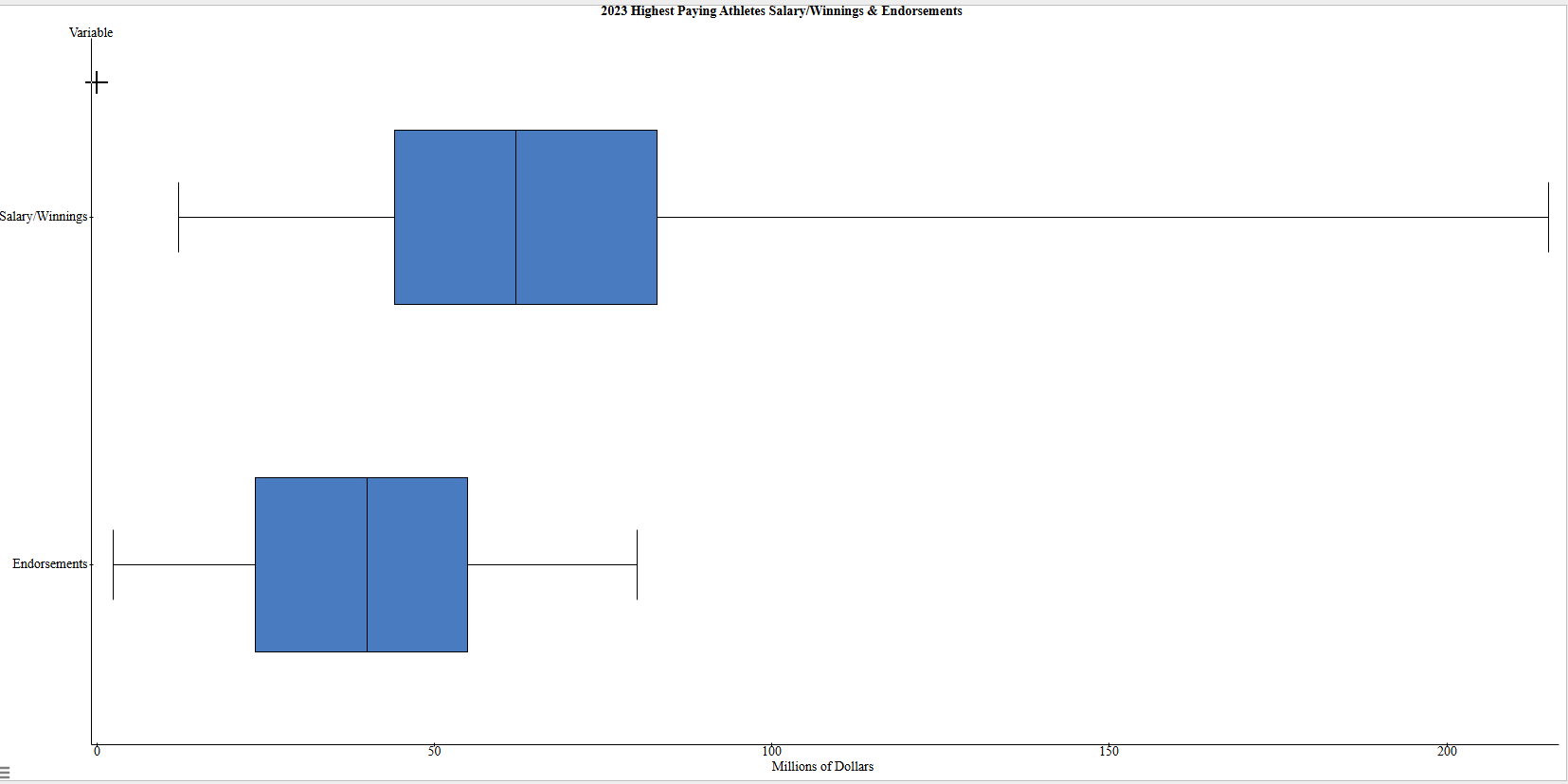
      5. Two box plots- the top one is Salary/Winnings and the bottom is Endorsements. The x-axis is labeled Millions of Dollars and goes from 0 to 200 counting by 50. Both are in millions of dollars. The 5-number summary Salary/Winnings is 12.2, 44.15, 62.15, 83, and 215. the 5-number summary for Endorsements is 2.5, 23.5, 40, 55, and 80.

    10. Outliers:

    are observed values that lie an abnormal distance from other values in a random sample from a population.

    In our course, outliers are defined as data values outside the boundaries of the max and min outlier critical values. Give the formulas for the outlier critical values:

    Outlier Calculations:

    • Lower Outlier Critical Value: \(Q_1 - 1.5(IQR)\)
    • Upper Outlier Critical Value: \(Q_3 + 1.5(IQR)\)
  10. Are there any outliers in the Total Earnings data set?
    1. What is the lower outlier critical value for the Total Earnings data set? 77.7 – 1.5(47.65) = $6.225 million
    2. Are there any data values in the Total Earnings data set that are less than your answer to part (a)? no
    3. What is the upper outlier critical value for the Total Earnings data set? 125.35 + 1.5(47.65) = $196.825 million
    4. Are there any data values in the Total Earnings data set that are greater than your answer to part (c)? Yes--Ronaldo with $275 M and Rahm with $203 M
  11. Are there any outliers in the Salary/Winnings data set? Yes--Ronaldo with $125 M and Rahm with $181 M
  12. Are there any outliers in the Endorsements data set? no

  13. The accompanying box-and-whisker plot represents the cost, in dollars, of twelve water bottles.

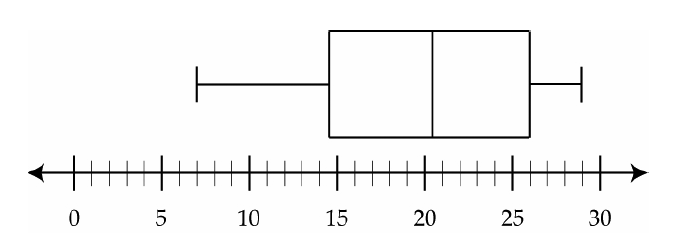
    The scale for the Box and Whisker plot is from 0 to 30 counting by 1. The low number is 7, the quartile 1 number is 14.5, the median is 20.5, the quartile 3 number is 26 and the high number is 29.The far left whisker is at 7. The far right whisker is at 29. The box is drawn with the left side at 14.5, the median at 20.5 and the right side at 26.

    1. Which cost is the upper quartile?

      2. $26

    2. What is the range of the costs of the water bottles?

      3. $22

    3. What is the median?

      4. $20.50

    4. Which cost represents the 100th percentile?

      5. $29

    5. How many water bottles cost between $14.50 and $26.00?

      6. 6

    6. How many water bottles cost less than $14.50?

      7. 3

  14. What percentage of values in the data set shown are greater than 6?

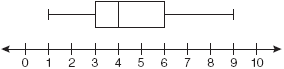
    The scale on the Box and Whisker plot is from 0 to 10 counting by 1. The low number on the plot is 1, the quartile 1 number is3, the median is 4, the quartile 3 number is 6 and the high number is 9.

    1. 25%
    2. 50%
    3. 75%
    4. 100%

    a. 25%

  15. A movie theater recorded the number of tickets sold daily for a popular movie during the month of June. The box-and-whisker plot shown below represents the data for the number of tickets sold, in hundreds.

    The scale on the Box and Whisker plot is from 0 to 10 counting by 1. The low number on the plot is 1, the quartile 1 number is 3, the median is 4, the quartile 3 number is 6 and the high number is 9.

    1. Which conclusion can be made using this plot?
      1. The second quartile is 600.
      2. The mean of the attendance is 400.
      3. The range of the attendance is 300 to 600.
      4. Twenty-five percent of the attendance is between 300 and 400.

      iv. Twenty-five percent of the attendance is between 300 and 400.

    2. Of the following ranges of daily tickets sales, which range of ticket sales occurred more often than the others?
      1. 100-300
      2. 300-500
      3. 400-600
      4. 600-900

      ii. 300-500 more than 25% of the daily ticket sales.

  16. The accompanying box-and-whisker plots can be used to compare the annual incomes of three professions.

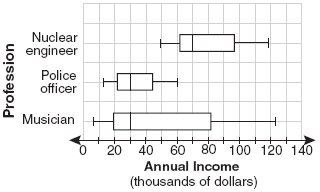
    The scale on the Box and Whisker plot is from 0 to 140 counting by 10. Each number represents the annual income in thousands of dollars. There are three plots. The first one is for the income for Nuclear Engineers. The low number is 50, the quartile 1 number is 60, the median is 70, the quartile 3 number is 100 and the high number is 120. The second plot is for the income for Police Officers. The low number is 12, the quartile 1 number is 22, the median is 30, the quartile 3 number is 43 and the high number is 60. The third plot is for the income for Musicians. The low number is 8, the quartile 1 number is 20, the median is 30, the quartile 3 number is 80 and the high number is 122.

    1. Based on the box-and-whisker plots, which statement is true?
      1. The median income for nuclear engineers is greater than the income of all musicians.
      2. The median income for police officers and musicians is the same.
      3. All nuclear engineers earn more than all police officers.
      4. A musician will eventually earn more than a police officer.

      ii. The median income for police officers and musicians is the same.

    2. At least how much income do 75% of musicians earn per year?

      $20,000