4.2 Hypothesis Testing for Proportions



We can use StatCrunch → Stat → Proportion Stats → One Sample → With Summary (or With Data) to test a claim about a population proportion p as long as the requirements are met:

  1. Driving and Texting: In a survey, 1864 out of 2246 randomly selected adults in the U.S. said that texting while driving should be illegal (based on data from Zogby International). Consider a hypothesis test that uses a 0.05 significance level to test the claim that more than 80% of adults believe that texting while driving should be illegal.
    1. Put a box around the statement of the claim in the problem. More than 80% of adults believe that texting while driving should be illegal.
    2. The original Claim: \(p>0.8\)
    3. \(H_0\): \(p \leq 0.8\) We will assume that \(p = 0.8\)
    4. \(H_A\): \(p > 0.8\)
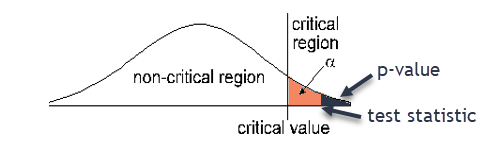
    5. Type of Test: Right-tailed test
    6. Draw a graph of the critical/rejection region

      7. A normal curve with a critical value marked with a vertical line alpha units from the right end of the graph. The area to the right of the critical value is shaded and labeled critical region. The area to the left of the critical value is not shaded and is labeled non-critical region.

    7. Significance Level \(\alpha\) (area of critical regions): \(\alpha =.05\)
    8. Sample proportion: \(\hat{p}=\frac{1864}{2246}=.83\)
    9. p-value: 0.0002
    10. Decision about the null:

      Since 0.0002 is less than 0.05, we reject the null hypothesis.

    11. Concluding statement:

      There is sufficient sample evidence to support the claim that more than 80% of adults believe texting while driving should be illegal.


      Claim has \( =,\ \ \le,\ \ \geq \) Claim has \( \neq,\ <,\ \ > \)
      Claim is null hypothesis Claim is alternate hypothesis
      Reject the null hypothesis “There is sufficient sample evidence to reject the claim that…” “There is sufficient sample evidence to support the claim that…”
      Fail to reject the null hypothesis “There is not sufficient sample evidence to reject the claim that…” “There is not sufficient sample evidence to support the claim that…”

  2. Cell phone and Cancer: In a study of 420,095 Danish cell phone users, 135 subjects developed cancer of the brain or nervous system (based on data from the Journal of the National Cancer Institute as reported in USA Today). Test the claim of a once popular belief that such cancers are affected by cell phone use. That is, test the claim that cell phone users develop cancer of the brain or nervous system at a rate that is different from the rate of 0.034% for people who do not use cell phones. Because this issue has such great importance, use a 0.01 significance level.
    1. Put a box around the statement of the claim in the problem. Cell phone users develop cancer of the brain or nervous system at a rate that is different from the rate of 0.034% for people who do not use cell phones.
    2. The original Claim: \(p \neq 0.00034\)
    3. \(H_0\): \(p = 0.00034\)
    4. \(H_A\): \(p \neq 0.00034\)
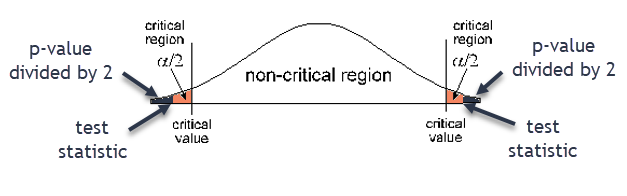
    5. Type of Test: Two-tailed test
    6. Draw a graph of the critical/rejection region

      7. A normal curve with two critical values marked with vertical lines alpha divided by 2 units from each end of the graph. The area to the left and right of the 2 critical values are shaded to the ends of the curve and labeled critical regions. The area between the critical values is not shaded and is labeled non-critical region.

    7. Significance Level \(\alpha\) (area of critical regions): \(\alpha =0.01\)
    8. Sample proportion: \(\hat{p}=\frac{135}{420095} \approx 0.00032\)
    9. p-value: 0.5122
    10. Decision about the null: Since 0.5122 is greater than 0.01, we fail to reject the null hypothesis
    11. Concluding statement: There is not sufficient sample evidence to support the claim that cell phone users develop cancer of the brain/nervous system at a rate different from non-cell phone users.

      12. Claim has \( =,\ \ \le,\ \ \geq \) Claim has \( \neq,\ <,\ \ > \)
      Claim is null hypothesis Claim is alternate hypothesis
      Reject the null hypothesis “There is sufficient sample evidence to reject the claim that…” “There is sufficient sample evidence to support the claim that…”
      Fail to reject the null hypothesis “There is not sufficient sample evidence to reject the claim that…” “There is not sufficient sample evidence to support the claim that…”

  3. Flu: In a clinical trial, 28 out of 800 patients taking a new prescription drug complained of flulike symptoms. Suppose that it is known that 2.2% of patients taking competing drugs complain of flulike symptoms. The company marketing the new drug is concerned about the rate of side effects. Test the claim that no more than 2.2% of the new drug’s users experience flulike symptoms as a side effect at the 0.1 significance level.
    1. Put a box around the statement of the claim in the problem. No more than 2.2% of this drug’s users experience flu-like symptoms as a side effect.
    2. Claim: \(p \leq 0.022\)
    3. \(H_0\): \(p \leq 0.022\)
    4. \(H_A\): \(p > 0.022\)
    5. Type of Test: Right-tailed test
    6. Draw a graph of the critical/rejection region

      A normal curve with a critical value marked with a vertical line alpha units from the right end of the graph. The area to the right of the critical value is shaded and labeled critical region. The area to the left of the critical value is not shaded and is labeled non-critical region.

    7. Significance Level \(\alpha\) (area of critical regions): \(\alpha =0.1\)
    8. p-value: 0.0061
    9. Decision about the null: Since 0.0061 is less than 0.10, we reject the null hypothesis.
    10. Concluding statement: There is sufficient sample evidence to reject the claim that no more than 2.2% of the drug’s users experience flu-like symptoms.

      11. Claim has \( =,\ \ \le,\ \ \geq \) Claim has \( \neq,\ <,\ \ > \)
      Claim is null hypothesis Claim is alternate hypothesis
      Reject the null hypothesis “There is sufficient sample evidence to reject the claim that…” “There is sufficient sample evidence to support the claim that…”
      Fail to reject the null hypothesis “There is not sufficient sample evidence to reject the claim that…” “There is not sufficient sample evidence to support the claim that…”

    4. Goldfish Smile Hypothesis Testing

    A decorative image of 6 goldfish crackers with the words Go Fish in the middle.

  4. Claim: The proportion of all goldfish with smiles is "less than, equal to, or greater than" (choose one) ______%
  5. Your claim: _________________________

    One possible choice is to claim that p > .50. The solutions on the rest of the activity will be based on this claim. However, this is not what you are required to choose when you complete this in class.

    6. H0: _______________ \( p \leq .50 \) p = .50

    Ha: _______________ \( p > 0.50\)

    \( \alpha = .05\)

  6. Sample Data
    1. Number of goldfish in your sample: n = _______________ 100
    2. Number of SMILING goldfish in your sample: x = _______________ 35
    3. \( \hat{p}=\frac{x}{n} \) (the sample proportion) = _______________ .35
  7. Test Statistic: _____________________-3

  8. p-value: ______________________0.9987

  9. Decision: __________________________________________________ Fail to reject the null hypothesis
  10. Concluding Statement:








    11. There is not sufficient evidence to support the claim that the proportion of all goldfish with smiles is greater than 50%.

    Confidence Intervals

    A decorative image of 3 goldfish crackers.

  11. Sample Data
    1. Number of goldfish in your sample: n = _______________ 100
    2. Number of SMILING goldfish in your sample: x = _______________ 35
    3. \( \hat{p}=\frac{x}{n} \) (the sample proportion) = _______________ .35
  12. Use the sample to construct a 95% confidence interval for the proportion of smiling goldfish.
    1. Best Point Estimate: _________________________0.35
    2. Find the 95% confidence interval estimate of the population proportion p.

      3. \( (0.257, 0.443) \)


    3. Find the margin of error (E) that corresponds to a 95% confidence level.

      E = ______________________ 0.093

  13. How does your confidence interval support the conclusion you made about your claim??
    14. Since the confidence interval tells us we are 95% confident that the true percentage of all smiling goldfish is between 25.7% and 44.3%, we do not have evidence to support the claim that more than 50% of goldfish are smiling.

    In a hypothesis test for a proportion, we can also calculate a critical value and a test statistic.

    • The critical value is the z-score associated with the significance level α. It defines the critical region.
    • The test statistic is the z-score associated with the p-value. The test statistic is a standardized value calculated from the sample. If the test statistic is in the critical region, then we reject the null hypothesis.
  14. Velcro Sneakers: It is claimed that more than 15% of sneakers that are sold attach with Velcro. A sample of 35 sneakers finds that 10 of them attach with Velcro. Test the claim using a 0.10 significance level.
    1. Put a box around the statement of the claim in the problem. More than 15% of sneakers that are sold attach with Velcro.
    2. Claim: \(p > 0.15\)
    3. \(H_0\): \(p \leq 0.15\)
    4. \(H_A\): \(p > 0.15\)
    5. Type of Test: Right-tailed test
    6. Draw a graph of the critical/rejection region

      A normal curve with a critical value marked with a vertical line alpha units from the right end of the graph. The area to the right of the critical value is shaded and labeled critical region. The area to the left of the critical value is not shaded and is labeled non-critical region.

    7. Significance Level \(\alpha\) (area of critical regions): \(\alpha =0.10\)
    8. Sample proportion: 10/35 = 0.286
    9. Critical value (label this on your graph) 1.64
    10. j. Test statistic (label this on your graph) 2.25

      If the test statistic is in the critical region, then reject the null hypothesis.

    11. Decision about the null: Reject the null hypothesis.
    12. Concluding statement: There is sufficient evidence to support the claim that more than 15% of sneakers that are sold attach with Velcro.

    Claim has \( =,\ \ \le,\ \ \geq \) Claim has \( \neq,\ <,\ \ > \)
    Claim is null hypothesis Claim is alternate hypothesis
    Reject the null hypothesis “There is sufficient sample evidence to reject the claim that…” “There is sufficient sample evidence to support the claim that…”
    Fail to reject the null hypothesis “There is not sufficient sample evidence to reject the claim that…” “There is not sufficient sample evidence to support the claim that…”