Unit 4 Hypothesis Testing

10.1 Goodness of Fit

Test the hypothesis that an observed frequency distribution fits or conforms to a claimed distribution


Notations:

Requirements:

  1. The data have been randomly selected
  2. The sample data consist of frequency counts for each of the different categories.
  3. For each category, the expected frequency is at least 5. (The expected frequency for a category is the frequency that would occur if the data actually have the distribution that is being claimed. No requirement that the observed frequency for each category must be at least 5.)

Test Statistic for a Goodness of Fit Test

We will get this value from technology, but it can be calculated by hand:

Calculating Expected Frequencies

Expected frequencies are equal: \(E=n / k\)

Expected frequencies are not equal: \(E=np\) (for each category)

\(\chi^{2}=\sum \frac{(O-E)^{2}}{E}\)

Null and Alternative Hypotheses

Using Technology for a Goodness of Fit Test:

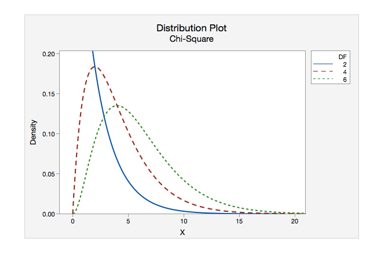
  1. Identify the critical chi-squared value, \({\chi^2}_{CV}\) (called \({\chi^2}_{O}\) in your text) in order to shade your curve.
    1. \(DF = k - 1\)
    2. Area to the right (always a right-tail test, use ≥) is the significance level

      Chi-square distribution plot: x-axis labeled from 0 to 20 in intervals of 5. Y-axis labeled from 0 to 0.2 in intervals of 0.05. There are 3 curves on the graph: one for 2 degrees of freedom, one for 4 degrees of freedom, and one for 6 degrees of freedom. The 2 DF graph is a solid black line that starts at the top of the graph (approximately (4, 0.20)) and drecreases rapidly to a horizontal asymptote of y=0. The 4 DF is graphed with large dashes. It begins at (0,0), climbs rapidly to approximately (4,0.18) and then descends slowly to a horizontal asypmtote at y=0. The 6 DF is graphed with small dashes. It begins at (0,0), climbs a little more slowly to approximately (5,0.13) and then descends slowly to a horizontal asypmtote at y=0.

  2. Run the test and record the important information: Identify
    1. Test Statistic (Chi-Square)
    2. P-value
  3. Mark your curve with your test statistic. Is it in the shaded rejection region in the right tail?
  4. Make your decision about the null. Was the p-value less than alpha?

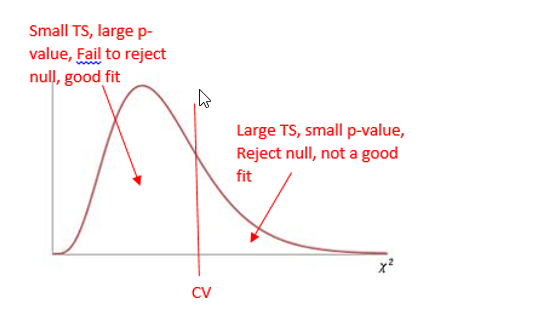
The Chi-Square Curve for a Goodness of Fit Test

Goodness-of-Fit is always a right-tailed test. Large values of χ^(2 )result from significant differences between observed and expected frequencies. When the test statistic falls in the critical region in the right tail, we know that our observed frequencies are too different from the claimed distribution for it to be a good fit.


Chi-square curve: Rises rapidly on the left side of the graph to the max and then slowly descends to the right. As a result, it looks like most of the graph is on the left. The critical value is labeled CV under the x-axis and marked with a vertical line through the curve. The larger area to the left of the CV is labeled Small TS, large p-value, fail to reject null, good fit. The smaller area to the right of the CV is labeled large TS, small p-value, reject null, not a good fit.

Problems

  1. College Dining : The college dining service claims there is no difference in student preferences among the following four entrees: pizza, cheeseburgers, chicken strips, and salad. A sample of 200 students showed that 61 preferred pizza, 49 preferred cheeseburgers, 54 preferred chicken, and 36 preferred salad. Use a 0.10 significance level to test the dining services claim that there is no difference in student preferences.
    Pizza Cheeseburger Chicken Strips Salad
    Number OBSERVED 61 49 54 36
    Number EXPECTED

    50

    50

    50

    50
    1. The original claim: There is no difference in student preferences among the four entrees—the preferences follow a uniform distribution.
    2. \(H_0\) : \(p_{1}=p_{2}=p_{3}=p_{4}\) The distribution of the four entrees is the same as the expected uniform distribution.
    3. \(H_A\) :The distribution of the four entrees differs from the expected uniform distribution.
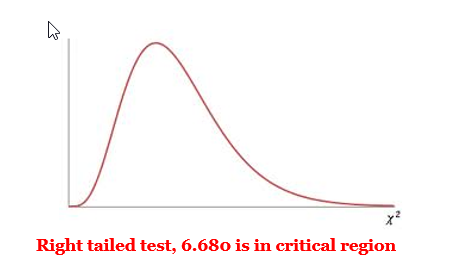
    4. \(\alpha\) = 0.10
    5. \({\chi^2}_{CV}\): = 6.251
    6. \({\chi^2}_{TS}\): = 0.641
    7. p-value: 0.0828
    8. Rejection Criteria: Reject \(H_0\) if p-value < 0.10
    9. Decision: Reject \(H_0\)

      10. Generic Chi-square curve labeled Right tailed test, 6.680 is in the critical region

    10. Concluding Statement:There is sufficient evidence to reject the claim that there is no difference in student preference between pizza, cheeseburgers, chicken strips, and salad.
    11. Describe the claimed distribution: Uniform
    12. Was it a good fit? No

  2. Ice-Cream Store (Different Expected Values for Each Category)

    An ice-cream store manager predicts the following distribution for the daily sale of the 6 flavors offered at his store in the month of January.

    Strawberry: 10%

    Cookie Dough: 20%

    Orange Sherbet: 10%

    Vanilla: 30%

    Mint Chocolate Chip: 10%

    Chocolate: 20%


    On January 10, his store sold the following scoops of ice-cream.

    Strawberry: 25 scoops

    Cookie Dough: 35 scoops

    Orange Sherbet: 20 scoops

    Vanilla: 50 scoops

    Mint Chocolate Chip: 30 scoops

    Chocolate: 40 scoops


    Test the store manager’s claim that the distribution of sales of the six flavors are his predicted values.

    Strawberry Cookie Dough Orange Sherbet Vanilla Mint Choc Chip Chocolate
    Observed 25 35 20 50 30 40
    Expected 20 40 20 60 20 40
    1. The original claim: The distribution of sales in the month of January is 10% Strawberry, 20% Cookie dough, 10% Orange Sherbet, 30% Vanilla, 10% Mint Chocolate chip, and 20% Chocolate.
    2. \(H_0\) : The distribution of flavors is the same as the expected distribution. \(p_{1}=.10, \quad p_{2}=.20,\quad p_{3}=.10,\quad p_{4}=.30,\quad p_{5}=.10, \quad p_{6}=.20\)
    3. \(H_A\) :The distribution of flavors differs from the expected distribution.
    4. \(\alpha\) = 0.05
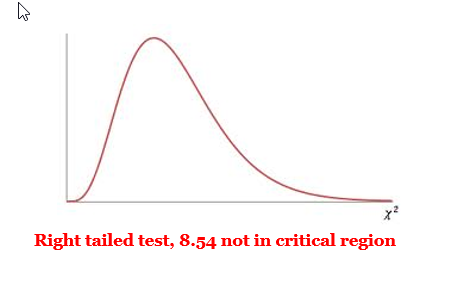
    5. \({\chi^2}_{CV}\): = 11.1
    6. \({\chi^2}_{TS}\): = 8.54
    7. p-value: 0.1288
    8. Rejection Criteria: Reject \(H_0\) if p-value < 0.05
    9. Decision: Fail to reject \(H_0\)

      10. Generic Chi-square curve labeled Right tailed test, 8.54 is in the critical region

    10. Concluding Statement: There is not sufficient evidence to reject the claimed distribution of ice cream sales.

  3. Blood Type: The proportions of blood types O, A, B, AB in the general population of a particular country are known to be in the ratio 49:38:9:4, respectively. A research team investigating a small isolated community in the country, obtained the frequencies of blood type given below. Test the hypothesis that the proportions in this community do not differ significantly from those in the country’s general population. Use a 0.05 significance level.
    Type O Type A Type B Type AB
    # selected OBSERVED 87 59 20 4
    # selected EXPECTED

    83

    65

    15

    7

    1. The original claim: The distribution of blood types in the community will be O (49%), A (38%), B (9%) and AB (4%).
    2. \(H_0\) : The distribution of the community sample is the same as the expected distribution. \(p_{1}=.49, p_{2}=.38, p_{3}=.09, p_{4}=.04\)
    3. \(H_A\) :The distribution of the community sample differs from the expected distribution.
    4. \(\alpha\) = 0.05
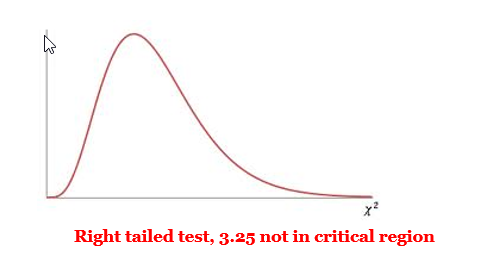
    5. \({\chi^2}_{CV}\): = 7.81
    6. \({\chi^2}_{TS}\): = 3.25
    7. p-value: 0.3552
    8. Rejection Criteria: Reject \(H_0\) if p-value < 0.05
    9. Decision: Fail to reject \(H_0\)

      10. Generic Chi-square curve labeled Right tailed test, 3.25 is in the critical region

    10. Concluding Statement: There is not sufficient evidence to reject the claim of a 49:38:9:4 distribution of blood types in the studied community.