Unit 1 Formula Sheet

Chapter 2


Standard Deviation:

Population

\(\sigma=\sqrt{\frac{\Sigma\left(x-\mu\right)^2}N}\)

Sample

\(s=\sqrt{\frac{\Sigma\left(x-\bar{x}\right)^2}{n-1}}\)

Frequency Distribution

\(s=\sqrt{\frac{\Sigma\left(x-\bar{x}\right)^2f}{n-1}}\)


z-Score:

Population

\(z=\frac{x-\mu}\sigma\)

Sample

\(z=\frac{x-\bar{x}}{s}\)

Empirical Rule:

(68-95-99.7 Rule) For symmetric, bell-shaped data sets

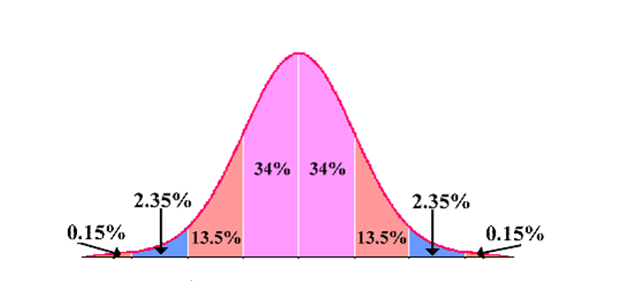
A normal curve with the x-axis labeled by integers from -3 to 3. The mean is labeled in the center of the x-axis at 0. The negative numbers to the left of the mean (-3 to -1) represent the standard deviations below the mean. The positive numbers to the right of the mean (1 to 3) represent the standard deviations above the mean. There are 8 shaded areas on the graph: four on each side of the mean. The graph is symmetric so the 4 areas to the left and right of the mean are mirror images of each other. From the left to the right of the graph the shaded areas represent the following percentages under the curve: 0.15%, 2.35%, 13.5%, 34%, 34%, 13.5%, 2.35%, and 0.15%

Range:

\(\text{Range}=\text{Maximum}-\text{Minimum}\)

Class Midpoint:

Class Midpoint = \(\frac{LCL+UCL}2\)

Class Width:

From raw data: \(\frac{ \text {Range} }{ \text {Number of Classes} }\) (round up)
From table: \( \text {Class Width} = LCL_2-LCL_1\)

Relative Frequency:

\( \text {Relative Frequency} = \frac{ \text {Class Frequency} }{ \text {Sample Size} } = \frac fn \)

Variance:

\( \text {variance} = \left( \text {standard deviation} \right)^2\)

Mean

Population

\(\mu=\frac{\Sigma x}N\)

Sample

\(\bar{x}=\frac{\Sigma x}n\)

Weighted

\(\bar{x}=\frac{\Sigma xw}{\Sigma w}\)

Frequency Distribution

\(\bar{x}=\frac{\Sigma xf}n\)

Interquartile Range and Outliers

Interquartile Range

\(IQR=Q_3-Q_1\)

Lower Outlier Critical Value:

\(Q_1-1.5(IQR)\)

Upper Outlier Critical Value:

\(Q_3+1.5(IQR)\)