Unit 2 Probability

3.3 The Addition Rule


Compound Events: Combining two or more simple events.

Mutually Exclusive (or Disjoint) events: Compound events that CANNOT OCCUR at the same time

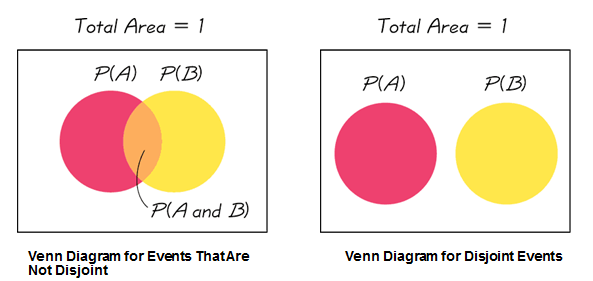
A picture of two Venn Diagrams. In the first Venn Diagram, titled Venn Diagram for events that are not disjoint, there are two intersecting circles. One circle represents P(A) and the other represents P(B). The intersection of the two circles represents P(A and B). In the second Venn Diagram, titled Venn Diagram for disjoint events, one circle represents P(A) and the other circle represents P(B). The two circles are not intersectimg each other.

The Addition Rule: Probability of Event A OR Event B occurring.

\(P(A \text { or } B)=P(A)+P(B)-P(A \text { and } B)\)

  1. In our bag of poker chips, what was P(B)?   P(1)?   What is P(Blue or 1)?

    \(P(B)=\frac{4}{9}\)

    \(P(1)=\frac{3}{9}\)

    To calculate P(Blue or 1), we will need P(Blue and 1): \(P(\text {Blue } \text {and } 1)=\frac{1}{9}\)

    \(P(B \text { or } 1)=P(B)+P(1)-P(B \text { and } 1)=\frac{4}{9}+\frac{3}{9}-\frac{1}{9}=\frac{6}{9}\)

  2. Let's roll 2 six-sided dice. n(S) = 36

    1 1 1 2 1 3 1 4 1 5 1 6
    2 1 2 2 2 3 2 4 2 5 2 6
    3 1 3 2 3 3 3 4 3 5 3 6
    4 1 4 2 4 3 4 4 4 5 4 6
    5 1 5 2 5 3 5 4 5 5 5 6
    6 1 6 2 6 3 6 4 6 5 6 6

    1. P (sum of 3) =

      \(\frac{2}{36}=.056\)

    2. P (sum of 7) =

      \(\frac{6}{36}=.167\)

    3. P (sum of 1) =

      \(\frac{0}{36}=0\)

    4. P (sum < 13 ) =

      \(\frac{36}{36}=1\)

    5. P (first die is 3) =

      \(\frac{6}{36}=.167\)

    6. P(second die is 5) =

      \(\frac{6}{36}=.167\)

    7. P (first is a 3 or second is a 5) =

      \(\frac{6}{36}+\frac{6}{36}-\frac{1}{36}=\frac{11}{36}\)

  3. With a standard deck of cards and a fair die, find the following probabilities:
    1. P(draw a heart and roll a 3)

      2. \(\frac{13}{52} \cdot \frac{1}{6}=\frac{13}{312}=.0417\)

    2. P(draw a face card and roll an odd number)

      3. \(\frac{12}{52} \cdot \frac{3}{6}=\frac{36}{312}=.1154\)

    3. P(draw a jack, given that you draw a face card)

      4. \(\frac{4}{12}=.333\)

    4. P(draw a heart or roll a three)

      5. \(\frac{13}{52}+\frac{1}{6}=.417\)

    5. P(draw a red or draw a ten)

      6. \(\frac{26}{52}+\frac{4}{52}-\frac{2}{52}=\frac{28}{52}=.5382\)

    6. P(draw a king or draw a diamond)

      7. \(\frac{4}{52}+\frac{13}{52}-\frac{1}{52}=\frac{4}{13}=.3077\)

  4. In a bag, you have

    4 blue chips numbered 1, 2, 3,and 4

    3 red chips numbered 1, 2, and 3

    2 green chips numbered 1 and 2.

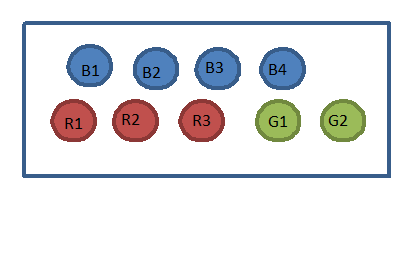
    A rectangle with 4 blue circles, three red circles and 2 green circles inside it.

    You randomly select one chip from the bag. Find:

    1. P (blue or red) \(P(B)+P(R)-P(B \text { and }R)=\frac{4}{9}+\frac{3}{9}-\frac{0}{9}=\frac{7}{9}=.7778\) B and R are disjoint events.
    2. P (blue or 3) \(P(B)+P(3)-P(B \text { and }3)=\frac{4}{9}+\frac{2}{9}-\frac{1}{9}=\frac{5}{9}=.5556\)
    3. P (red or 3) \(P(R)+P(3)-P(R \text { and }3)=\frac{3}{9}+\frac{2}{9}-\frac{1}{9}=\frac{4}{9}=.4444\)
    4. P (green or 3) \(P(G)+P(3)-P(G \text { and }3)=\frac{2}{9}+\frac{2}{9}-\frac{0}{9}=\frac{4}{9}=.4444\)

    5. Using the Addition Rule with a Contingency Table
  5. The following table gives the number of people with health insurance coverage in the U.S. in 2018. Note that the numbers are in millions of people.

    Source of data
    (In millions) Private insurance Private insurance (Marketplace) Public Insurance Uninsured Total Number
    Adults age 18-64 128.2 8.4 38.5 26.4

    201.5
    Children age 0-17 38.5 1.7 30.7 3.8

    74.7
    Total Number

    166.7

    10.1

    69.2

    30.2

    276.2

    Find the probabilities if you randomly select one person:

    1. P(Adult) =

      \(\frac{n(E)}{n(S)}=\frac{201.5}{276.2}=.7395\)

    2. P(Uninsured) =

      \(\frac{30.2}{276.2}=.1093\)

    3. P(Adult and Uninsured) =

      \(\frac{26.4}{276.2}=.0956\)

    4. P(Adult or Uninsured) =

      \(P(\text {adult})+P(\text {uninsured})-P(\text { adult } A N D \text { uninsured })=\frac{201.5}{276.2}+\frac{30.2}{276.2}-\frac{26.4}{276.2}=\frac{205.3}{276.2}=.7433\)

      5. Group Discussion:

    5. P(Child) =

      \(\frac{74.7}{276.2}=.2705\)

    6. P(public insurance) =

      \(\frac{69.2}{276.2}=.2505\)

    7. P(private insurance) =

      \(\frac{166.7}{276.2}+\frac{10.1}{276.2}=\frac{176.8}{276.2}=.6401\)

    8. P(Child or private insurance) =

      \(\frac{74.7}{276.2}+\frac{176.8}{276.2}-\frac{40.2}{276.2}=\frac{211.3}{276.2}=.7650\)

    9. P(Child or no private insurance)

      \(P(\text {child}) + P(\text {private insurance}) - P(\text {child AND private insurance}) =\frac{74.7}{276.2}+\frac{99.4}{276.2}-\frac{34.5}{276.2}=\frac{139.6}{276.2}=.5054\)