Unit 4 Hypothesis Testing

7.3 Hypothesis Testing for the Mean


Step 4:

Identify Level of Significance and Degrees of Freedom

Identify Test Statistic for Mean Claim:

Step 5: Using the P-value to Evaluate the Null Hypothesis

Definition of P-value: The probability of being as extreme, or more extreme, than your data, assuming H0 is correct.

Step 6: Determine the Rejection Region

Step 7: Make One of Two Decisions About the Null Hypothesis


  1. If P-value \(\leq \alpha\):
    • reject \(H_0\)
    • Type I error: rejecting \(H_0\) when it is actually true
  2. If P-value \(> \alpha\):
    • fail to reject \(H_0\)
    • Type II error: failing to reject \(H_0\) when it is actually false

Step 8: Formulate a Conclusion About the Claim

Null is the Claim Alternate is the Claim
Reject the Null “There is sufficient sample evidence to reject the claim that…” “There is sufficient sample evidence to support the claim that…”
Fail to Reject the Null “There is not sufficient sample evidence to reject the claim that…” “There is not sufficient sample evidence to support the claim that…”


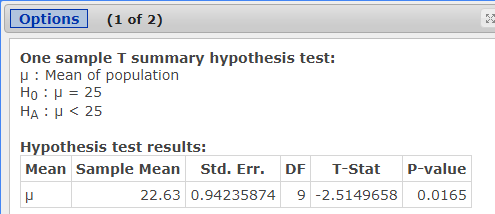
  1. Changing a Tire: The length of time to change a tire is normally distributed. A random sample of ten tire changes is taken with a mean of 22.63 minutes and a standard deviation of 2.98 minutes. Use a 0.05 significance level to test the claim that the mean time to change a tire is less than 25 minutes.
    1. Design the Study
      1. The original Claim: \(\mu < 25\)
      2. \(H_0\): \(\mu \geq 25\) assume \(H_0\): \(\mu = 25\)
      3. \(H_A\): \(\mu < 25\)
      4. Type of Test: Left-tailed test
      5. Level of Significance: \(\alpha =.05\)
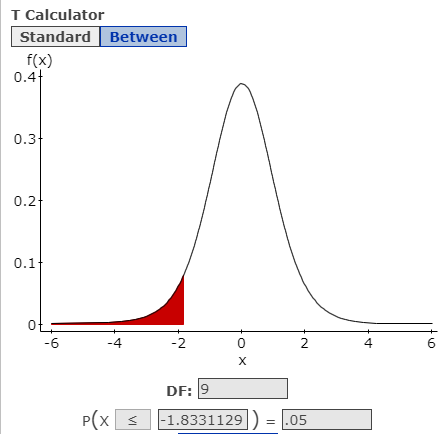
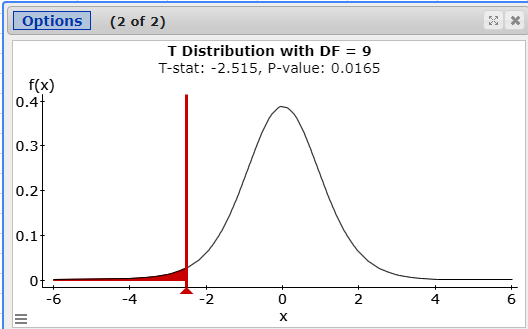
      6. Degrees of Freedom: \(10-1=9\)
      7. Critical Value(s): \(t=-1.8331\) Determines shaded area(s)

      T calculator with the graph of a normal curve. The x-axis is labeled from -6 to 6 in intervals of 2. The top of the curve is at x=0. The y-axis is labeled from 0 to 0.4 in intervals of 0.1. The area under the curve is shaded for all x values less than -1.8331129. Under the graph, there is a box with df:9 and under that a box with P(x<=-1.8331129)=.05

    2. Results
      1. Test Statistic: A standardized value based on the sample data, assuming the null is true.

        \(t=\frac{\overline{x}-\mu}{\left(\frac{s}{\sqrt{n}}\right)}=\frac{22.63-25}{\left(\frac{2.98}{\sqrt{10}}\right)}=-2.5150\)

      2. p-value: 0.0165
      3. Rejection Criteria: Reject \(H_0\) if p value \(< \alpha\) and the test statistic (t) is in the rejection region.
      4. Decision about the null: Reject \(H_0\)

        Reason 1: 0.0165 < .05 or Reason 2: -2.5150 is in the rejection region

      5. Concluding statement about the claim: There is sufficient evidence to support the claim the mean time to change a tire is less than 25 minutes.

      One sample T summary hypothesis test: mu: mean of the population, H_O: mu = 25, H_A: mu < 25. Hypothesis Test results: Mean: mu Sample Mean: 22.63 Std. Err.: 0.94235874 DF: 9 T-Stat: -2.5149658 p-value: 0.0165

      Graph of t-distribution with DF=9, T-stat=-2.515, p-value: 0.0165. T calculator with the graph of a normal curve. The x-axis is labeled from -6 to 6 in intervals of 2. The top of the curve is at x=0. The y-axis is labeled from 0 to 0.4 in intervals of 0.1. The area under the curve is shaded for all x values less than -2.515.

  2. Age of Cars: The mean age of cars driven by Pellissippi State students is seven years. The Dean of Students claims that this is an accurate statement for his students. A random sample of 31 cars in the East Parking Lot on campus showed a mean age of 8.1 years with a standard deviation of 5.1 years. Test the Dean’s claim at the 0.01 significance level.
    1. Design the Study
      1. The original Claim: \(\mu = 7\)
      2. \(H_0\): \(\mu = 7\) assume \(H_0\): \(\mu = 7\)
      3. \(H_A\): \(\mu \neq 7\)
      4. Type of Test: Two-tailed test
      5. Level of Significance: \(\alpha =.01\)
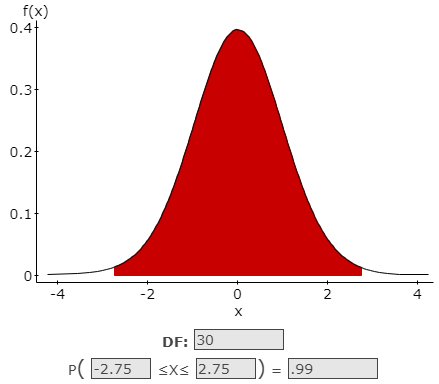
      6. Degrees of Freedom: \(31-1=30\)
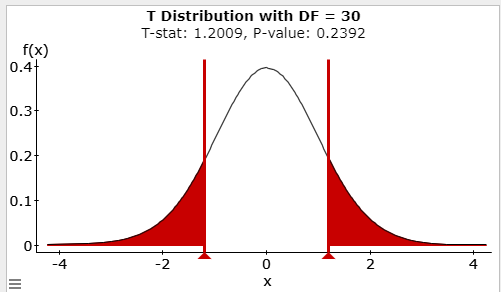
      7. Critical Value(s): \(t=\pm 2.750\) Determines shaded area(s)

      T calculator with the graph of a normal curve. The x-axis is labeled from -4 to 4 in intervals of 2. The top of the curve is at x=0. The y-axis is labeled from 0 to 0.4 in intervals of 0.1. The area under the curve is shaded for all x values between -2.75 and +2.75. Under the graph, there is a box with df:30 and under that a box with P(-2.75<=x<=2.75)=.99

    2. Results
      1. Test Statistic: A standardized value based on the sample data, assuming the null is true.

        \(\mathrm{t}=\frac{\overline{x}-\mu}{\left(\frac{s}{\sqrt{n}}\right)}=\frac{8.1-7}{\left(\frac{5.1}{\sqrt{31}}\right)}=1.20089\)

      2. p-value: 0.2392
      3. Rejection Criteria: Reject \(H_0\) if

        p value \(< \alpha\) and the test statistic (t) is in the rejection region.

      4. Decision about the null: Fail to reject \(H_0\)

        Reason 1: 0.2392 > .01

        Reason 2: 1.20089 is not in the rejection region
      5. Concluding statement about the claim: There is not sufficient evidence to reject the claim the mean age of cars driven by PSCC students is 7 years.

      One sample T summary hypothesis test: mu: mean of the population, H_O: mu = 7, H_A: mu does not equal 7. Hypothesis Test results: Mean: mu Sample Mean: 8.1 Std. Err.: 0.91598704 DF: 30 T-Stat: 1.2008904 p-value: 0.2392

      Graph of t-distribution with DF=30, T-stat=1.2009, p-value: 0.2392. T calculator with the graph of a normal curve. The x-axis is labeled from -4 to 4 in intervals of 2. The top of the curve is at x=0. The y-axis is labeled from 0 to 0.4 in intervals of 0.1. The area under the curve is shaded for all x values less than -1.2009 and greater than +1.2009.

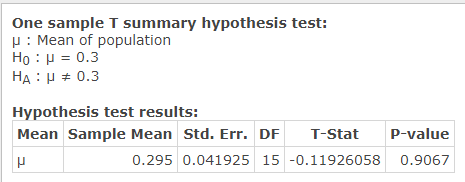
  3. Sugars in Cereal: In a sample of 16 cereals, the mean sugar content was measured at .295g and the standard deviation was .1677g. Use a .01 significance level to test the claim the true population mean sugar content (grams of sugar per gram of cereal) for all cereals is equal to 0.3g.
    1. Design the Study
      1. The original Claim: \(\mu = 0.3\)
      2. \(H_0\): \(\mu = 0.3\) assume \(H_0\): \(\mu = 0.3\)
      3. \(H_A\): \(\mu \neq 0.3\)
      4. Type of Test: Two-tailed test
      5. Level of Significance: \(\alpha =0.01\)
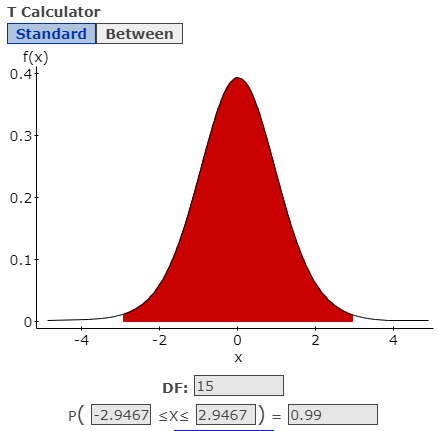
      6. Degrees of Freedom: \(16-1=15\)
      7. Critical Value(s): \(t=\pm 2.947\) Determines shaded area(s)

      T calculator with the graph of a normal curve. The x-axis is labeled from -4 to 4 in intervals of 2. The top of the curve is at x=0. The y-axis is labeled from 0 to 0.4 in intervals of 0.1. The area under the curve is shaded for all x values between -2.947 and +2.947. Under the graph, there is a box with df:15 and under that a box with P(-2.9467<=x<=2.9467)=.99

    2. Results
      1. Test Statistic: A standardized value based on the sample data, assuming the null is true.

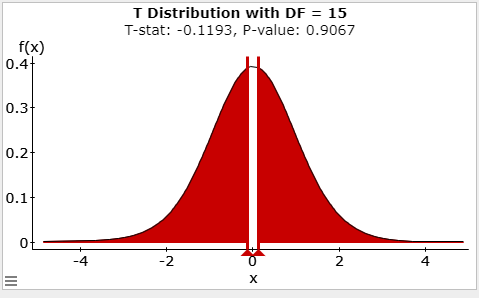
        \(t= \frac{\overline{x}-\mu}{\left(\frac{s}{\sqrt{n}}\right)} = \frac{.295-.3}{\left(\frac{.1677}{\sqrt{16}}\right)} =-0.1193\)

      2. p-value: 0.9067
      3. Rejection Criteria: Reject \(H_0\) if p value \(< \alpha\) and the test statistic (t) is in the rejection region.
      4. Decision about the null: Fail to reject \(H_0\)

        Reason 1: 0.9067 > .01

        Reason 2: -0.1193 is not in the rejection region

      5. Concluding statement about the claim: There is not sufficient evidence to reject the claim the true mean sugar content for all cereals is equal to 0.3g.

      One sample T summary hypothesis test: mu: mean of the population, H_O: mu = 0.3, H_A: mu does not equal 0.3. Hypothesis Test results: Mean: mu Sample Mean: 0.295 Std. Err.: 0.041925 DF: 15 T-Stat: -0.11926058 p-value: 0.9067

      Graph of t-distribution with DF=15, T-stat=-0.1193, p-value: 0.9067. T calculator with the graph of a normal curve. The x-axis is labeled from -4 to 4 in intervals of 2. The top of the curve is at x=0. The y-axis is labeled from 0 to 0.4 in intervals of 0.1. The area under the curve is shaded for all x values less than -0.1193 and greater than +0.1193.

  4. Class Size: You receive a brochure from a large university. The brochure indicates that the mean class size for full-time faculty is fewer than 31 students. You want to test this claim. You randomly select 18 classes taught by full-time faculty and determine the class size of each. The results are shown in the table below. At a 0.01 significance level, can you support the university’s claim?
    34 26 28 33 32 37 28 25 29
    26 28 37 30 31 25 29 31 28
    Sample Statistics: \(\overline{x}=29.8333333 \quad s=3.666221 \quad n=18\)
    1. Design the Study
      1. The original Claim: \(\mu < 31\)
      2. \(H_0\): \(\mu \geq 31\) assume \(H_0\): \(\mu = 31\)
      3. \(H_A\): \(\mu < 31\)
      4. Type of Test: Left-tailed test
      5. Level of Significance: \(\alpha =0.01\)
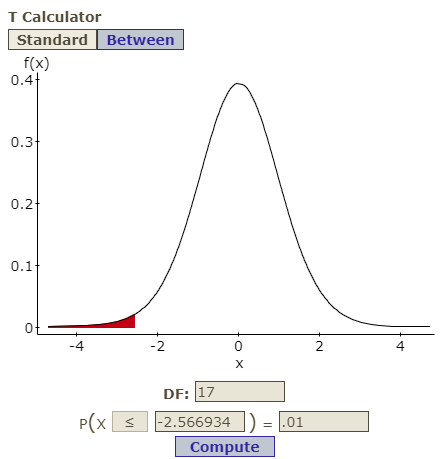
      6. Degrees of Freedom: \(18-1=17\)
      7. Critical Value(s): \(t=-2.5669\) Determines shaded area(s)

      T calculator with the graph of a normal curve. The x-axis is labeled from -4 to 4 in intervals of 2. The top of the curve is at x=0. The y-axis is labeled from 0 to 0.4 in intervals of 0.1. The area under the curve is shaded for all x values less than -2.5669. Under the graph, there is a box with df:17 and under that a box with P(x<=-2.566934)=.01

    2. Results
      1. Test Statistic: A standardized value based on the sample data, assuming the null is true.

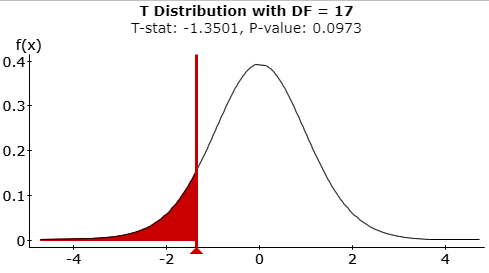
        \(t =\frac{\overline{x}-\mu}{\left(\frac{s}{\sqrt{n}}\right)} = \frac{29.833333-31}{\left(\frac{3.66621}{\sqrt{18}}\right)}=-1.3501\)

      2. p-value: 0.0973
      3. Rejection Criteria: Reject \(H_0\) if p value \(< \alpha\) and the test statistic (t) is in the rejection region.
      4. Decision about the null: Fail to reject \(H_0\)

        Reason 1: 0.0973 > .01

        Reason 2: -1.3051 is not in the rejection region

      5. Concluding statement about the claim: There is not sufficient evidence to support the claim the mean class size for full time faculty is fewer than 31 students.

      One sample T summary hypothesis test: mu: mean of the population, H_O: mu = 31, H_A: mu < 31. Hypothesis Test results: Mean: mu Sample Mean: 29.833333 Std. Err.: 0.86413658 DF: 17 T-Stat: -1.3500952 p-value: 0.0973

      Graph of t-distribution with DF=17, T-stat=-1.3501, p-value: 0.0973. T calculator with the graph of a normal curve. The x-axis is labeled from -4 to 4 in intervals of 2. The top of the curve is at x=0. The y-axis is labeled from 0 to 0.4 in intervals of 0.1. The area under the curve is shaded for all x values less than -1.3501.

Concluding Activity

Goldfish Smile Hypothesis Testing

Claim: The proportion of all goldfish with smiles is "less than, equal to, or greater than" 50% (choose one)

Your claim: _________________________

One possible choice is to claim that p > .50. The solutions on the rest of the activity will be based on this claim. However, this is not what you are required to choose when you complete this in class.

Sample Data

Number of goldfish: n = _______________ 100

Number of SMILING goldfish: x = _______________ 35

\( \hat{p} \) = _______________ .35

H0: _______________ \( p \leq .50 \) assume H0: _______________ p = .50

Ha: _______________ \( p > 0.50

\( \alpha = .05\)

Test Statistic

z = General Formula = Specific Formula = Numeric Value

\( z = \frac{ \hat{p} - p}{\sqrt{\frac{pq}{n}}} = \frac{.35-.5}{ \sqrt{ \frac{(.5)(.5)}{100}}} = -3 \)

p-value: _______________ .9987

Rejection Criteria: Reject H0 if _____________________________________________ p-value < .05 z > 1.64

Decision: __________________________________________________ Fail to reject the null hypothesis

Concluding Statement:

_______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________-

______________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________________

There is not sufficient evidence to support the claim that the proportion of all goldfish with smiles is greater than 50%.

Use the sample to construct a 95% confidence interval for the proportion of smiling goldfish.

Best point esitmate: _______________ .35

Find the margin of error E that corresponds to a 95% confidence level.

E = _______________ .0935

Find the 95% confidence interval estimate of the population proportion p. \( .2565 \leq p \leq .4435 \)

How does your confidence interval indicate the decision you should make about whether or not you should reject H0?

.50 is within the confidence interval, so fail to reject H0.

Comparing Hypothesis Testing for the Mean and Hypothesis Testing for a Proportion

Mean T-test Proportion Z-test
Question It is claimed that the average time it takes to eat an apple is less than 4 minutes. A random sample of 25 apple eaters takes an average of 3.8 minutes to eat an apple with a standard deviation of 2.1 minutes. Test the claim using a 0.05 significance level. It is claimed that more than 15% of sneakers that are sold attach with Velcro. A sample of 135 sneakers finds that 26 of them attache with Velcro. Thest the claim using a 0.10 significance level.
Hypothesis Claim: \( \mu < 4 \)

H0: \( \mu \geq 4 \)

HA: \( \mu < 4 \)

Claim: \( p > .15 \)

H0: \( p \leq .15 \)

HA: \( p > .15 \)

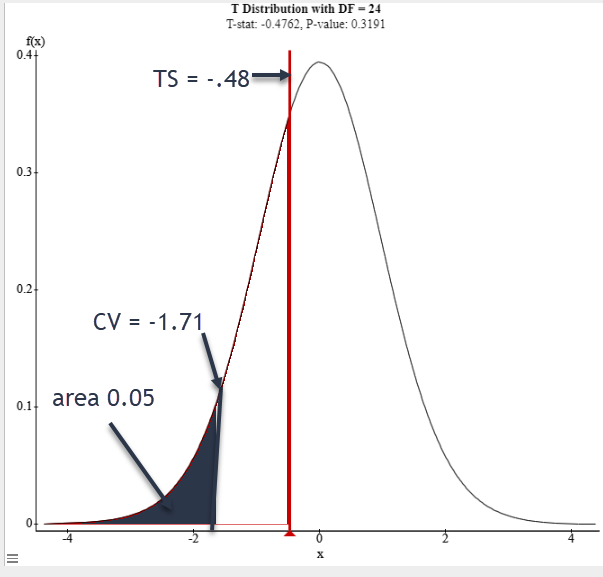
Critical Value(s)

-1.71

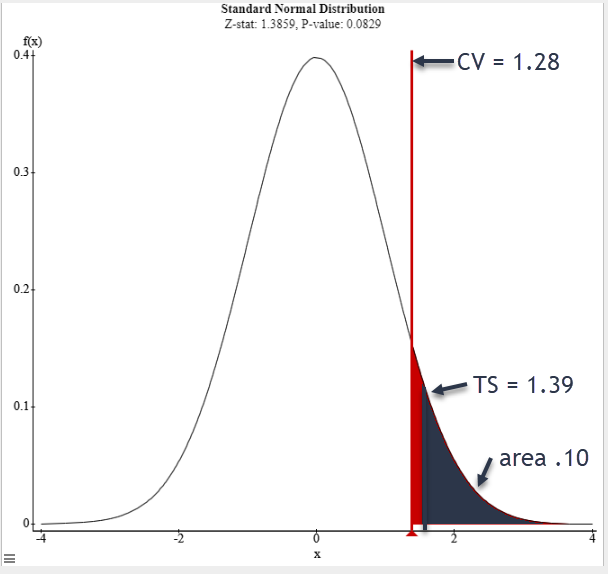
1.28
Test Statistic \( t = \frac{\bar{x} - \mu}{ \frac{s}{ \sqrt{n}}} = \) -.48 \( z = \frac{ \hat{p} - p}{ \sqrt{ \frac{pq}{n}}} = \) 1.39
Sketch the graph, label TS, CV, shade rejection region

A standard normal distribution graph. The area under the curve is shaded to the left of the critical value, -1.71. A line is drawn to show the test statistic at -0.48. Becasue the test statistic is not in the shaded rejection region, we fail to reject the null hypothesis.

A standard normal distribution graph. The area under the curve is shaded to the right of the critical value, 1.28. A line is drawn to show the test statistic at 1.39. Since the test statistic is in the shaded rejection region, we reject the null hypothesis.

P-Value 0.3191 0.0829
Decision (circle one) Reject H0

Fail to Reject H0

Fail to reject H0

 Reject H0

Fail to Reject H0

Reject H0
Conclusion

There is not sufficient evidence to support the claim that the mean time to eat an apple is less than 4 minutes.

There is sufficient evidence to support the claim that more than 15% of sneakers attach with Velcro.