Unit 1 Describing Data

Review

  1. Determine whether the data are qualitative or quantitative:
    1. the colors of automobiles on a used car lot qualitative
    2. the numbers on the shirts of a soccer team qualitative
    3. the number of seats in a movie theater quantitative
    4. a list of house numbers on your street qualitative
    5. the ages of a sample of 350 employees of a large hospital quantitative
  2. Identify the data set’s level of measurement (nominal, ordinal, interval, ratio):
    1. hair color of players on a high school tennis team nominal
    2. numbers on the shirts of a soccer team nominal
    3. ages of students in a statistics class ratio
    4. temperatures of 22 selected refrigerators interval
    5. number of milligrams of tar in 28 cigarettes ratio
    6. number of pages in your statistics book ratio
    7. marriage status of the faculty at the local community college nominal
    8. the rank of a winning Super Bowl team in their division ordinal
    9. the ratings of a movie ranging from “poor” to “good” to “excellent” ordinal
    10. the final grades (A,B,C,D, and F) for students in a chemistry class ordinal
    11. the annual salaries for all teachers in Utah ratio
    12. list of zip codes for Chicago nominal
    13. the nationalities listed in a recent survey nominal
    14. the amount of fat (in grams) in 44 cookies ratio

  3. Here we list the 20 countries that emitted the most carbon dioxide in 2015. Construct the following using the data: Frequency Distribution, Relative Frequency Distribution, Cumulative Frequency Distribution, Histogram, Dot Plot, Stem and Leaf. For the frequency distribution use a class width of 3 and 0 - 2.9 as the first class.
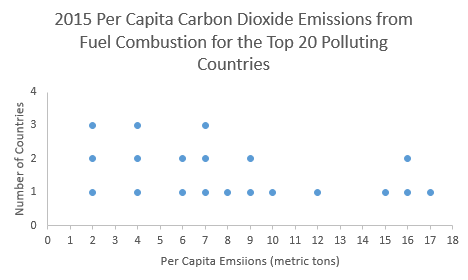
    Rank and Country 2015 Per Capita Carbon Dioxide Emissions from Fuel Combustion (metric tons)
    1 China 6.6
    2 United States 15.5
    3 India 1.6
    4 Russia 10.2
    5 Japan 9.0
    6 Germany 8.9
    7 South Korea 11.6
    8 Iran 7.0
    9 Canada 15.3
    10 Saudia Arabia 16.9
    11 Brazil 2.2
    12 Mexico 3.7
    13 Indonesia 1.7
    14 south Africa 7.8
    15 United Kingdom 6.0
    16 Australia 15.8
    17 Italy 5.5
    18 Turkey 4.1
    19 France 4.4
    20 Poland 7.3

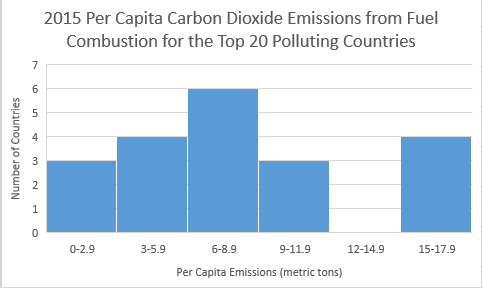
    Frequency
    EMISSIONS FREQUENCY

    0 – 2.9

    3

    3 - 5.9

    4

    6 - 8.9

    6

    9 - 11.9

    3

    12 - 14.9

    0

    15 - 17.9

    4
    Relative Frequency
    EMISSIONS RELATIVE
    FREQUENCY

    0 - 2.9

    15%

    3 – 5.9

    20%

    6 - 8.9

    30%

    9 - 11.9

    15%

    12 - 14.9

    0%

    15 - 17.9

    20%
    Cumulative Frequency
    EMISSIONS CUMULATIVE
    FREQUENCY

    0 - 2.9

    3

    3 - 5.9

    7

    6 - 8.9

    13

    9 - 11.9

    16

    12 - 14.9

    16

    15 - 17.9

    20
    Stem Leaves

    1

    6  7

    2

    2

    3

    7

    4

    1  4

    5

    6

    0  6

    7

    0  3  8

    8

    9

    9

    0

    10

    2

    11

    6

    12

    13

    14

    15

    3  5  8

    16

    9

    Legend 16

    9 = 16.9

    A histogram representing the 2015 Per Capita Carbon Dioxide Emissions from Fuel Combustion for the Top 20 Polluting Countries. The horizontal axis represents the classes of per capita emissions in metric tons. The classes are 0-2.9, 3-5.9, 6-8.9, 9-11.9, 12-14.9, and 15-17.9. The vertical axis represents the number of countries in each class and goes from 0 to 7 counting by 1. The number in each class is 3,4,6,3,0, and 4 respectively.

    A dot plot representing the 2015 Per Capita Carbon Dioxide Emissions from Fuel Combustion for the Top 20 Polluting Countries. The horizontal axis represents the per capita emissions in metric tons. It starts at 0 and ends at 18, counting by 1. The horizontal axis represents the number of countries and goes from 0 to 4, counting by 1. There are 3 dots at 2 metric tons, 3 dots at 4 metric tons, 2 dots at 6 metric tons, 3 dots at 7 metric tons, 1 dot at 8 metric tons, 2 dots at 9 metric tons, 1 dot at 12 metric tons, 1 dot at 15 metric tons, 2 dots at 16 metric tons, and 1 dot at 17 metric tons.

  4. Below is a random sample of life expectancies from 20 countries:
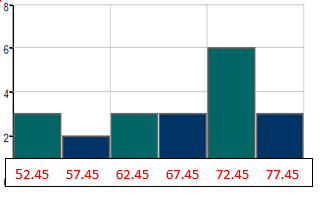
    70.5 65 70 51.5 57.5 61 78.5 61 72 64.5
    56.5 73 69 52.5 78.5 54 74.5 76 70 68.5
    1. Make a frequency table of the life expectancies.

      Use a starting lower class limit of 50.0 and a class width of 5.0.

      Class Frequency

      50.0 – 54.9

      3

      55.0 – 59.9

      2

      60.0 – 64.9

      3

      65.0 – 69.9

      3

      70.0 – 74.9

      6

      75.0 – 79.9

      3

    2. Answer the following questions based on your histogram:
      1. What are the class midpoints?

        52.45, 57.45, 62.45, 67.45, 72.45, 77.45

      2. What are your lower class limits?

        50.0, 55.0, 60.0, 65.0, 70.0, 75.0

      3. What are your upper class limits?

        54.9, 59.9, 64.9, 69.9, 74.9, 79.9

      4. Draw a histogram using the class midpoints:

        A histogram representing the life expectancies of people in 20 countries. The horizontal axis is the midpoint of each class: 52.45, 57.45, 62.45, 67.45, 72.45, and 77.45. The vertical axis is numbered from 0 to 8 counting by 2. The first bar is at 3, the second one at 2, the third one at 3, the fourth one at 3, the fifth one at 6 and the last one at 3.

      5. Use the same data to create a relative frequency distribution:
        Classes Relative Frequency

        50.0 - 54.9

        3/20 = 15%

        55.0 - 59.9

        2/20 = 10%

        60.0 - 64.9

        3/20 = 15%

        65.0 - 69.9

        3/20 = 15%

        70.0 - 74.9

        6/20 = 30%

        75.0 - 79.9

        3/20 = 15%
  5. Use the following data to complete a-e:

    AIDS data indicating the number of months a patient with AIDS lives after taking a new antibody drug are as follows (smallest to largest):

    3 4 8 8 10 11 12 13 14 15
    15 16 16 17 17 18 21 22 22 24
    24 25 26 26 27 27 29 29 31 32
    33 33 34 34 35 37 40 44 44 47
    1. Calculate the measures of center from the given list of numbers.

      Mean: 23.6

      Median: 24

      Mode: multi-modal

      Midrange: 25

    2. Create a frequency table using 2 as the lower limit of the first class and a class width of 8.
      CLASS FREQUENCY

      2 - 9

      4

      10 - 17

      11

      18 - 25

      7

      26 - 33

      10

      34 - 41

      5

      42 - 49

      3
    3. ESTIMATE the mean of the data using the frequency table. Mean = 23.5
    4. ESTIMATE the median of the data using the frequency table. First, identify the position of the median. Which CLASS in the frequency table contains the median?

      The position of the median is 41/2 = 20.5, so the 21st term, which is in the third CLASS 18 - 25.

  6. These are the volumes (in ounces) of randomly selected cans of Coke:
    12.3 12.0 12.1 12.3 12.2 12.3 12.2
    1. Find the Mean, median, mode, midrange. Mean = 12.2 Median = 12.2 Mode = 12.3 Midrange = 2.15
    2. Find the mean of the following frequency distribution:
      GPA FREQUENCY

      CLASS MIDPOINT

      Frequency x Midpoint
      0 - 0.9 4

      0.45

      1.8
      1 - 1.9 7

      1.45

      10.15
      2 - 2.9 12

      2.45

      29.4
      3 - 3.9 15

      3.45

      51.75
      4 - 4.9 6

      4.45

      26.7

      SUM = 44

      SUM = 119.8

      119.8/44 = 2.72

      MEAN = 2.72

    3. What is the shape of the data represented in the frequency distribution?

      Skewed to the left

  7. The ages of the employees at a local newspaper are given. Use the data to complete a-d:
    20 26 52 30 21 36 34 60 57 51 56 63 42
    1. Calculate the measures of variation from the given list of numbers. Range = 43 Variance = 232.6 Standard Deviation = 15.3
    2. Create a frequency table using 20 as the lower limit of the first class and a class width of 10.
      CLASS FREQUENCY

      MIDPOINT

      20 -29

      3

      24.5

      30 - 39

      3

      34.5

      40 - 49

      1

      44.5

      50 - 59

      4

      54.5

      60 - 69

      2

      64.5
    3. ESTIMATE the mean of the ages using the frequency table. Mean = 43.7
    4. ESTIMATE the standard deviation of the ages using the frequency table. Standard Deviation = 15.0

  8. Use the frequency table to estimate the mean and standard deviation of ticketed speeds:
    Speed in mph of Driver
    Ticketed in 30 mph Zone    		 Frequency of Speed
    Reported on the Ticket

    Midpoint
    42 - 45 10

    43.5
    46 - 49 14

    47.5
    50 - 53 7

    51.5
    54 - 57 3

    55.5
    58 - 61 1

    59.5
    1. Estimate the mean of the data: Mean = 48.2
    2. Estimate the standard deviation of the data: Standard Deviation = 4.2

    9. FIVE-NUMBER SUMMARIES AND PERCENTILES

  9. The circumference measurements (in cm) of a sample of randomly selected trees on a farmer’s property is given below. Use the data to answer the following questions.
    18 18 19 24 31 34 37 37 38 39
    40 41 49 51 51 52 53 55 83 112
    1. CALCULATE THE FOLLOWING

      Mean: 44.1

      Median: 39.5

      Mode: 18, 37, 51

      MidRange: 65

      Range: 94

      Variance: 492.8

      Standard Deviation: 22.2

      Q1: 32.5

      Q3: 51.5

      IQR: 51.5 - 32.5 = 19

      Are there any outliers in the data?

      Yes, 83 and 112 are outliers

      Lower Outlier Limit: Q1 – 1.5*IQR   32 – 1.5*19 = 4

      Any data point less than 4 is an outlier.

      Upper Outlier Limit: Q3 + 1.5*IQR   51.5 + 1.5*19 = 80

      Any data point greater than 80 is an outlier.

    2. CREATE A BOXPLOT OF THE DATA: Mark outliers clearly on the boxplot.

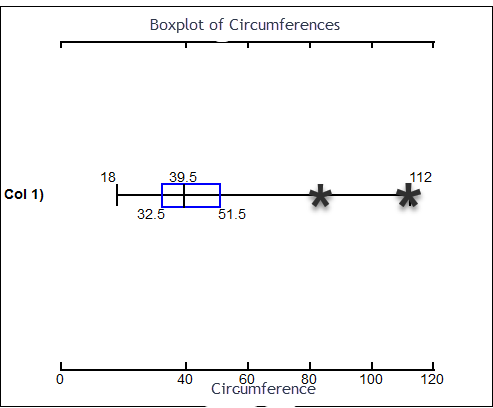
      A box and whisker plot with a 5 number summary of 18, 32.5, 39.5, 51.5, and 112. There are 2 outliers on the right side of the graph.

    3. What is the Percentile of 24? 15th percentile

      \(\frac{3}{20} \times 100=15\)

  10. The average life expectance of a specific brand of tires is 40,000 miles and has a mound shaped distribution (bell-shaped). The standard deviation is 7,500 miles.
    1. Construct and label a bell curve representing the distribution.

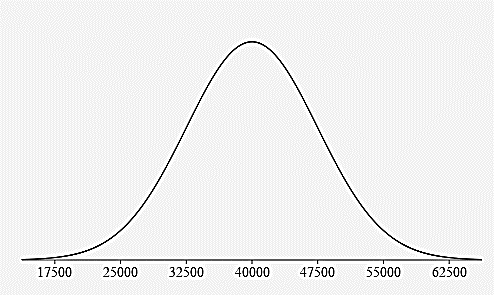
      A bell shaped curve. The horizontal axis is numbered 17500 to 62500, counting by 7500.

    2. What percentage of all tires have a life expectancy that is:

      Below 32,500 miles? 16%     0.15% + 2.35% + 13.5%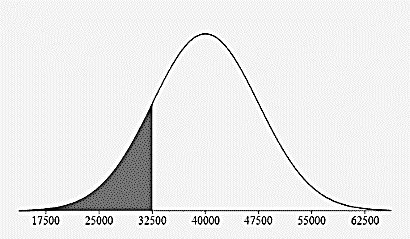

      A bell shaped curve. The horizontal axis is numbered 17500 to 62500, counting by 7500.The area under the curve between 17500 and 32500 is shaded.

      Above 25,000 miles? 97.5%     13.5% + 34% + 34% 13.5% + 2.35% + 0.15%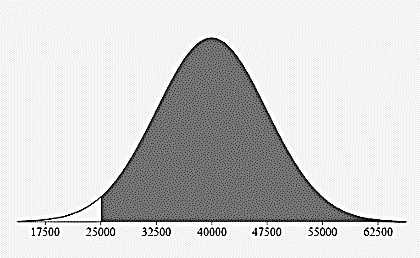

      A bell shaped curve. The horizontal axis is numbered 17500 to 62500, counting by 7500. The area under the curve between 25000 and 62500 is shaded.

      Between 40,000 and 55,000 miles? 47.5%     34% + 13.5%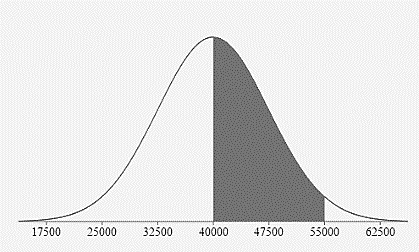

      A bell shaped curve. The horizontal axis is numbered 17500 to 62500, counting by 7500.The area under the curve between 40000 and 55000 is shaded.

  11. According to dairymoos.com, the mean weight of an adult cow is 1500 lb. Assuming the weights are normally distributed with a standard deviation of 180lb,
    1. Construct and label a bell curve representing the distribution.

      A bell shaped curve that is numbered from 960 to 2040, counting by 180.

    2. What percentage of adult cows weigh:

      Between 1320 pounds and 1860 pounds? 81.5%     34% + 34% + 13.5%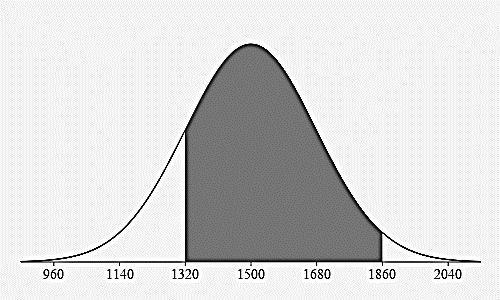

      A bell shaped curve that is numbered from 960 to 2040, counting by 180. The area under the curve between 1320 and 1860 is shaded.

      Less than 1500 pounds? 50%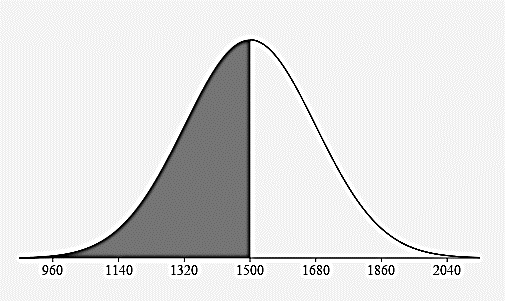

      A bell shaped curve that is numbered from 960 to 2040, counting by 180. The area under the curve between 960 and 1500 is shaded.

      More than 1680 pounds? 16%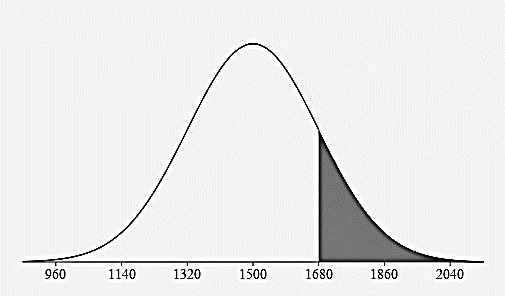

      A bell shaped curve that is numbered from 960 to 2040, counting by 180. The area under the curve between 1680 and 2040 is shaded.

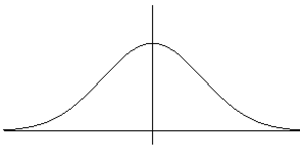
  12. Heights of women in the population have a bell-shaped distribution with a mean of 161cm and a standard deviation of 7cm. If one woman is randomly selected, what is the probability her height will be: A bell shaped curve with no labels.
    1. less than 168 cm? 84%
    2. greater than 147 cm? 97.5%
    3. between 154 cm and 168 cm? 68%
    4. between 147 cm and 175 cm? 95%

      5. Z SCORES

    5. Find a z score for a woman that is 156 cm tall: \(z_{156}=\frac{156-161}{7}=-0.71\)
    6. What does this z-score mean in words:

      The woman’s height of 156 cm is 0.71 standard deviations below the mean of 161 cm.

    7. Find a z score for a woman that is 170 cm tall: \(z_{170}=\frac{170-161}{7}=1.29\)
    8. What does this z-score mean in words:

      The woman’s height of 170 cm is 1.29 standard deviations above the mean of 161 cm.

    9. Find a z score for a woman that is 161 cm tall: \(z_{161}=\frac{161-161}{7}=0\)
    10. What does this z-score mean in words:

      The woman’s height of 161 cm is 0 standard deviations above or below the mean of 161 cm.

  13. According to MarathonGuide.com, in 2010 the average time it took to run a marathon was about 4.5 hours with a standard deviation of about 1 hour.
    1. Construct and label a bell curve representing the distribution.

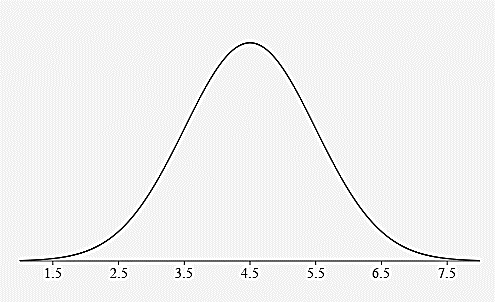
      A bell shaped curve. The horizontal axis is numbered 1.5 to 7.5, counting by 1.

    2. Find the z-score for a runner who finishes in 3.2 hours \(z_{3.2}=\frac{3.2-4.5}{1}=-1.3\)
    3. What does this z-score mean in words:

      A runner’s time of 3.2 hours is 1.3 standard deviations below the mean time of 4.5 hours. (faster than average)

    4. Find the z-score for a runner who finishes in 5.2 hours: \(z_{5.2}=\frac{5.2-4.5}{1}=0.7\)
    5. What does this z-score mean in words:

      A runner’s time of 5.2 hours is 0.7 standard deviations above the mean time of 4.5 hours. (slower than average)

    6. Would you consider someone who finishes a marathon in 2 hours and 15 minutes to be very fast? What would their z-score be and what does that mean? hours and 15 minutes = 2.25 hours (because 15 minutes is ¼ of an hour)

      \(z_{2.25}=\frac{2.25-4.5}{1}=-2.25\)

      A runner’s time of 2.25 hours is 2.25 standard deviations below the mean time of 4.5 hours. This runner’s time would be more than 2 standard deviations below the mean and would be considered unusually fast.

  14. Review of Frequency Distributions
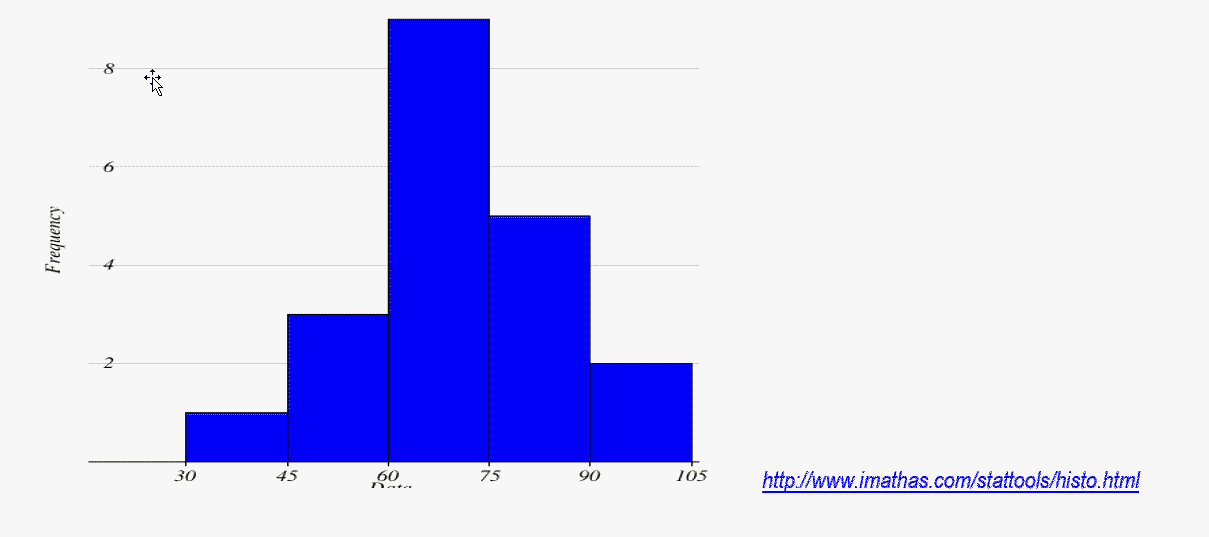
    1. Use the data to construct a Frequency Distribution Table: Begin with a lower class limit of 30 and a class width of 15.

      32   49   53   57   61   64   66   68   68   68   71   72   72   75   79   80   83   85   90   93

      CLASS FREQUENCY RELATIVE FREQUENCY
      30- 44

      1

      0.05

      45-59

      3

      0.15

      60-74

      9

      0.45

      75-89

      5

      0.25

      90-104

      2

      0.10

      Cumulative Class Cumulative Frequency

      Less than 45

      1

      Less than 60

      4

      Less than 75

      13

      Less than 90

      18

      Less than 105

      20
    2. Find the following using the Frequency Table (not the Relative or Cumulative summary information):
      • •Lower Class Limit of the 3rd Class 60
      • Lower Class Boundary of the 3rd Class 59.5
      • Midpoint of the 3rd Class 67
    3. Use the Frequency Distribution (not Relative or Cumulative) to draw a Histogram of the data:

      A frequency distribution (bar graph) with the x-axis labeled from 30 to 105 in intervals of 15. The frequency is labeled on the y-axis from 0 to 8 in intervals of 2. The first bar goes from 30 to 45 with a height of 1. The second bar goes from 45 to 60 with a height of 3. The third bar goes from 60 to 75 with a height of 9. The fourth bar goes from 75 to 90 with a height of 5, and the fifth and final bar goes from 90 to 105 with a height of 2.