MATH 1530

Unit 2 Probability

3.1 Basic Concepts of Probability and Counting

Basic Probability

Calculating the Probability of an Event

\(P(E)=\frac{\# \text { of Possible Successes}}{\text {Total } \# \text { of Possible Outcomes}}=\frac{n(E)}{n(S)}\)

1. In a bag, you have
   • 4 blue chips numbered 1, 2, 3, & 4
   • 3 red chips numbered 1, 2, & 3
   • 2 green chips numbered 1 & 2

   

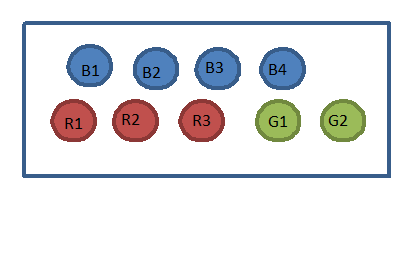
   You randomly select one chip from the bag. Find:

   Event	Theoretical Probability	Experimental Probability
   P(B) n(E)=n(Blue)=4 n(S)=n(Chips)=9	\(\frac{4}{9}=.444=44.4 \%\)
   P(R)	\(\frac{3}{9}=.333=33.3 \%\)
   P(G)	\(\frac{2}{9}=.222=22.2 \%\)
   P(4)	\(\frac{1}{9}=.111=11.1 \%\)
   P(3)	\(\frac{2}{9}=.222=22.2 \%\)
   P(\(\overline{B}\)) = P(not blue)	\(\frac{5}{9}=.556=55.6 \%\)
   P(\(\overline{R}\))	\(\frac{6}{9}=.667=66.7 \%\)
   P(\(\overline{G}\))	\(\frac{7}{9}=.778=77.8 \%\)
   P(number less than 5)	\(\frac{9}{9}=1=100 \%\)
   P(5)	\(\frac{0}{9}=0=0 \%\)




Complements Rule

What do you notice about P(\(B\)) and P(\(\overline{B}\))? \(P(B)+P(\overline{B})=\frac{4}{9}+\frac{5}{9}=1\)

What do you notice about P(\(R\)) and P(\(\overline{R}\))? \(P(R)+P(\overline{R})=\frac{3}{9}+\frac{6}{9}=1\)





Probability Rules for Complements

1. \(P(A)+P(\overline{A})=1\)
2. \(P(A)=1-P(\overline{A})\)
3. \(P(\overline{A})=1-P(A)\)

Some Special Probabilities

Impossible Event: probability of 0

Certain Event: probability of 1

Unusual Event: probability is very low

2. You roll a fair 6-sided die
   1. List the Sample Space: \((S)=\{1,2,3,4,5,6\}\)     \(n(S)=6\)
   2. What is the probability of:
      1. rolling an odd number greater than 1?

         \(P(E)=\frac{n(E)}{n(S)}\)

         Sample space: \(E=\{3,5\}\)     \(n(E)=2\)   \(P(E)=\frac26=\frac13\)

      2. not rolling an odd number greater than one?

         This is a good example when to use the Rule of Complements. The problem above is the complement of this problem.

         P(not rolling odd greater than 1) = 1 - P(rolling odd greater than 1) \(=1-\frac{2}{6}=\frac{4}{6}\)

         \(E=\{1,2,4,6\} ; n(E)=4\)

      3. rolling a value greater than 6? \(\frac{0}{6} ; E=\{ \}\) impossible
      4. rolling a value between 1 and 6, inclusive? \(\frac{6}{6} ; E\{1,2,3,4,5,6\} \) certain
      5. rolling a value between 1 and 6? \(E={2,3,4,5} \) so the probability is \(\frac{4}{6}=\frac23\)

Creating the List of Outcomes for a Large Sample Space



3. You are ordering salad at Panera. You will select between 4 salads as your entrée. The 4 salads are: Chicken Cobb with Avocado, Thai Chicken, Strawberry Poppyseed with Chicken, and Fuji Apple Chicken. You have three choices for side items: chips, apple or baguette. List the different outcomes for your sample space if your meal will consist of one salad and one side item.

   

   

   

   

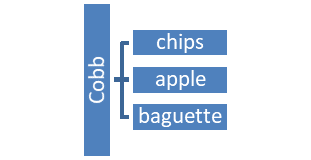
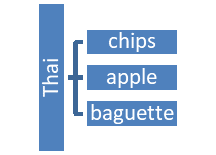
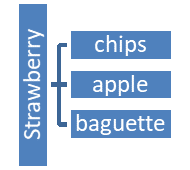
   1. How many possible outcomes do we have in our sample space? \(n(S)=4 \times 3=12\)  4 salads, 3 sides
   2. You decide to add a drink. Your choices are: Coke, Diet Coke, Sprite, Sweet Tea and UnSweet Tea. Now how many outcomes are in your sample space? \(n(S)=4 \times 3 \times 5=60\)  4 salads, 3 sides, 5 drinks

Fundamental Counting Principle:

For a sequence of two events in which the first event can occur in m ways and the second event can occur in n ways, the events together can occur in m*n ways. This rule can be extended to any number of events occurring in sequence.

4. You are choosing an outfit to wear to school. You have 10 shirts, 5 pairs of pants, and 3 pairs of shoes. How many outfits can you make?

   \(10 \times 5 \times 3=150\) outfits

5. An access code consists of six characters. For each character, any letter or number can be used, with the exceptions that the first character cannot be 0, and the last two characters must be odd numbers.

   \(35 \times 36 \times 36 \times 36 \times 5 \times 5=40824000\)

6. What is the probability of randomly selecting the correct access code on the first try? \(\frac{1}{40824000}=0.0000000245\)

   The TI calculator output will be \(2.45E-8\)

Fair Game Activity

Figure This! Two players each roll ordinary six-side die. Of the two numbers showing, the smaller is subtracted from the larger. If the difference is 0, 1, or 2, Player A gets 1 point. If the difference is between 3, 4, or 5, Player B gets 1 point. The game ends after 12 rolls. The player with the most points wins the game. Is this game fair?

Record the data below. Hint use tally marks to keep track of who wins each of the 12 rolls.

OUR DATA:

CLASS DATA:

Do you think this game is fair?

1. Prove by theoretical probability your answer to whether the game is fair. Use the sample space below to determine, if both players roll a die, the probability Player A will win the point and the probability Player B will win the point.

   1 1	1 2	1 3	1 4	1 5	1 6
   2 1	2 2	2 3	2 4	2 5	2 6
   3 1	3 2	3 3	3 4	3 5	3 6
   4 1	4 2	4 3	4 4	4 5	4 6
   5 1	5 2	5 3	5 4	5 5	5 6
   6 1	6 2	6 3	6 4	6 5	6 6

2. Develop rules for a game that is fair. You may use the sample space below to prove your game is fair. (Highlight outcomes where A wins with your rules and where B wins with your rules.)

   1 1	1 2	1 3	1 4	1 5	1 6
   2 1	2 2	2 3	2 4	2 5	2 6
   3 1	3 2	3 3	3 4	3 5	3 6
   4 1	4 2	4 3	4 4	4 5	4 6
   5 1	5 2	5 3	5 4	5 5	5 6
   6 1	6 2	6 3	6 4	6 5	6 6