Linear Modeling and Logic Unit

4.8 and 4.9 Review


Venn Diagrams and Deductive Arguments


  1. Draw a Venn Diagram to represent the following information and answer the questions.

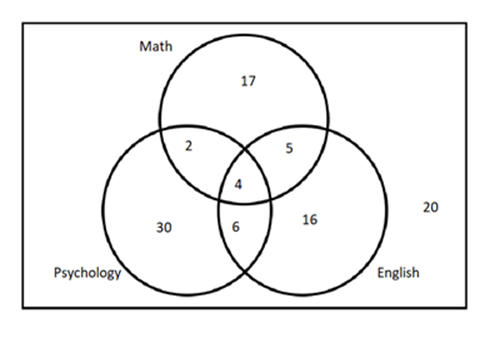
    100 college freshmen were interviewed

    28 students were registered for a math class

    31 students were registered for an English class

    42 students were registered for a Psychology class

    9 students were registered for both math and English

    10 students were registered for both English and Psychology

    6 students were registered for both math and Psychology

    4 students were registered for all three types of classes

    1. How many students took none of these three subjects?

      2. 20

    2. How many students took math, but not English or Psychology?

      3. 17

    3. How many students took math and English, but not Psychology?

      4. 5

    2. Blank Venn Diagram enclosed in a rectangle with three intersecting circles.

    A Venn Diagram enclosed in a rectangle that represents the universal set and contains 3 intersecting circles. One circle represents math, one represents English and one represents Psychology. There are numbers that represent the number of students in each section of the diagram. The number 17 is in math only, the number 30 is in Psychology only and the number 16 is in English only. The number 2 is in the intersection of math and Psychology. The number 5 is in the intersection of math and English. The number 6 is in the intersection of Psychology and English. The number 4 is in the intersection of all three circles and the number 20 is outside all three circles and inside the rectangle.

    Using a Venn diagram, determine if the following arguments are valid or invalid.

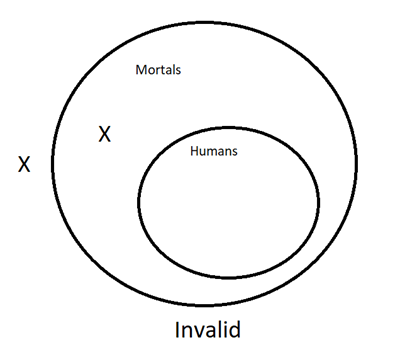
  2. Premise: All humans are mortal.

    Premise: Cassie is not human.

    Conclusion: Cassie is not mortal.

    3. A Venn Diagram with a small circle completely enclosed inside a large circle. The large circle represents mortals and the small circle represents humans. There is an X in the mortals circle but not inside the humans circle. There is also an X outside both circles. The argument is invalid.

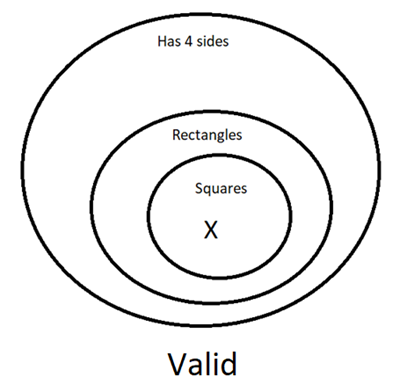
  3. Premise: All squares are rectangles.

    Premise: All rectangles have four sides.

    Conclusion: All squares have four sides.

    4. A Venn Diagram with three nested circles. The largest circle represents having 4 sides. The next size circle represents rectangles and the smallest circle represents squares. There is an X inside the circle representing squares. The argument is valid.

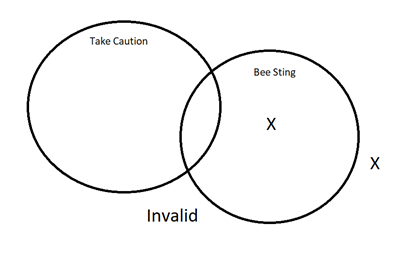
  4. Premise: Some bees may sting you when you do not take caution around them.

    Premise: Taylor was not careful when she played in the field where many bees are known to reside.

    Conclusion: Taylor was stung by a bee.

    5. A venn Diagram with two intersecting circles. One circle represents taking caution and the other circle represents getting a bee sting. There is an X in side the bee sting circle, but not in the intersection of the two circles. There is also an X outside both circles. The argument is invalid.

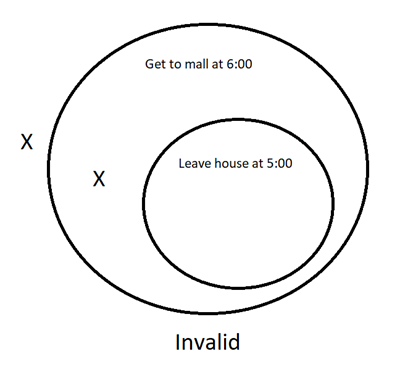
  5. Premise: If I leave my house at 5:00pm, I will get to the mall at 6:00pm.

    Premise: I left my house at 5:30pm.

    Conclusion: I made it to the mall by 6:00pm.

    6. A Venn Diagram with a small circle completely enclosed inside a large circle. The large circle represents getting to the mall at 6. The small circle represents leaving the house at 5. There is an X inside the large circle that is not in the small circle and there is an X that is outside both circles. The argument is invalid.

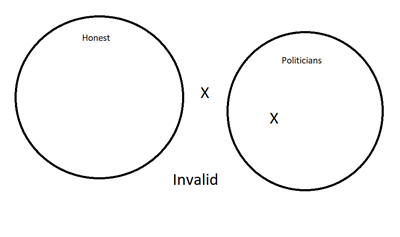
  6. Premise: There are no politicians who are honest.

    Premise: Garrett Poindexter is a dishonest man.

    Conclusion: Garrett Poindexter is a politician.

    7. A Venn Diagram with two disjoint circles. One circle represents being honest and the other circle represents politicians. There is an X inside the politicians circle and an X outside both circles. The argument is invalid.