Linear Modeling and Logic Unit

4.1 Rate of Change


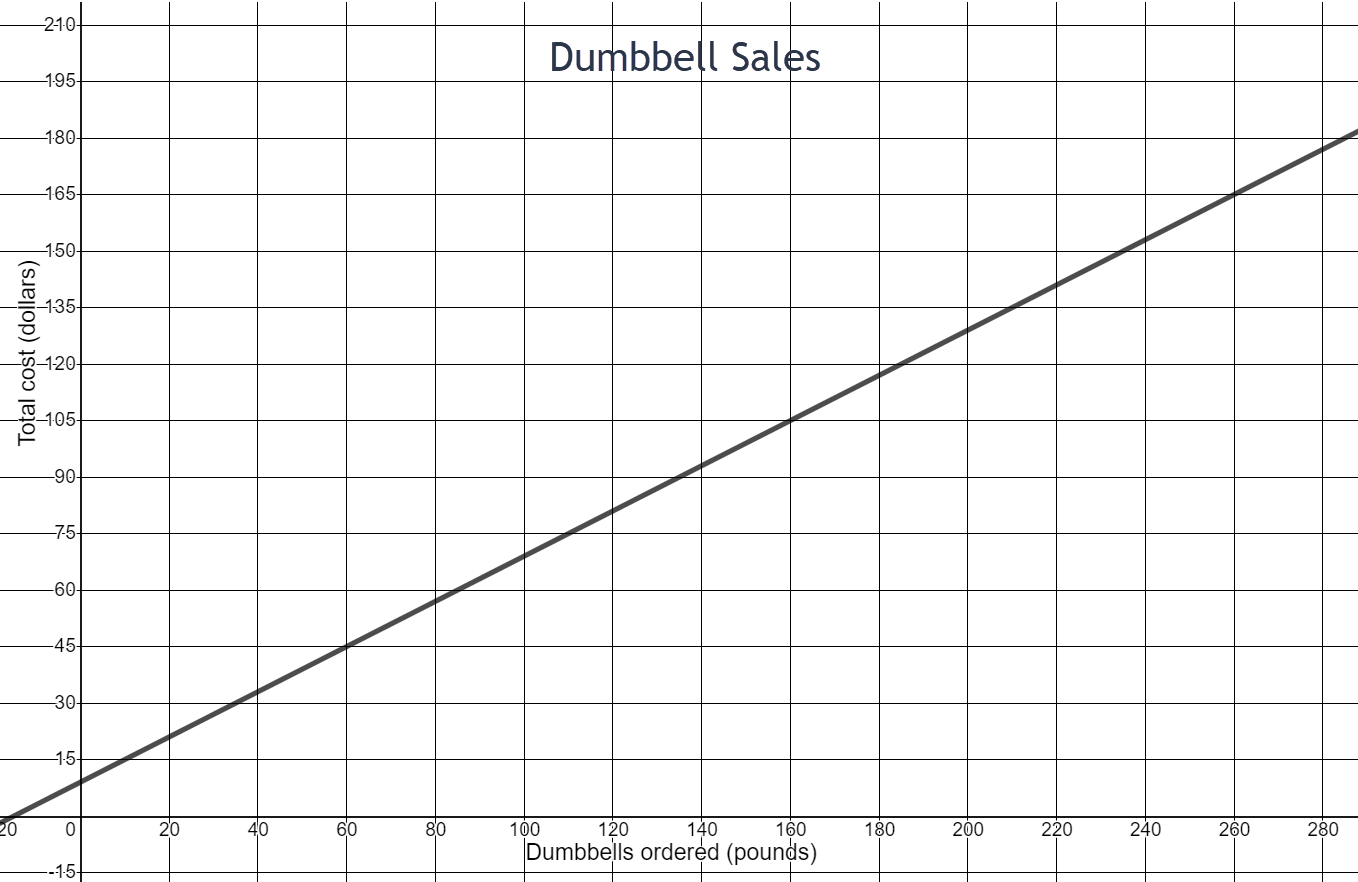
  1. Coordinate plane graph of Dumbbell Sales. A line increasing from left to right is graphed. The horizontal axis for Dumbbells ordered in pounds is numbered from zero to 300 by twenties. The vertical axis for Total Cost in dollars is numbered from zero to 225 by fifteens. The line starts at the point (0,9) and passes through points (60,45) and (160,105).

    1. What is the total cost for 60 pounds of dumbbells ordered? Write this as an ordered pair.

      2. (60,45)

    2. What is the total cost for 160 pounds of dumbbells ordered? Write this as an ordered pair.

      3. (160,105)

    3. How much more does it cost for 160 pounds of dumbbells compared to 60 pounds? Write this rate of change in fraction form.

      4. \(\begin{equation} \frac{105-45}{160-60}=\frac{\$60}{100 \text{ lbs}}=\frac{\$3}{5 \text{ lbs}} \end{equation}\)

    4. How much more do you pay for each additional pound ordered?

      5. $.60

    5. What is the initial cost of ordering dumbbells? (Look at the y-intercept where dumbbells ordered is 0 pounds.) What might this initial cost represent?

      6. $9 Could be the cost of shipping or processing fee or the cost of a weight bar.

      \begin{equation}\text{slope} =\frac{\text { vertical change }}{\text { horizontal change }} \end{equation}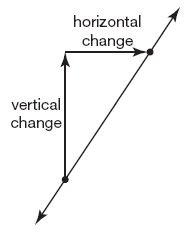
      A line increasing from left to right. Two points on the line are connected with a vertical line segment and a horizontal line segment that make a right triangle with the line as the hypotenuse. The vertical line segment is called the vertical change. The horizontal line segment is called the horizontal change.

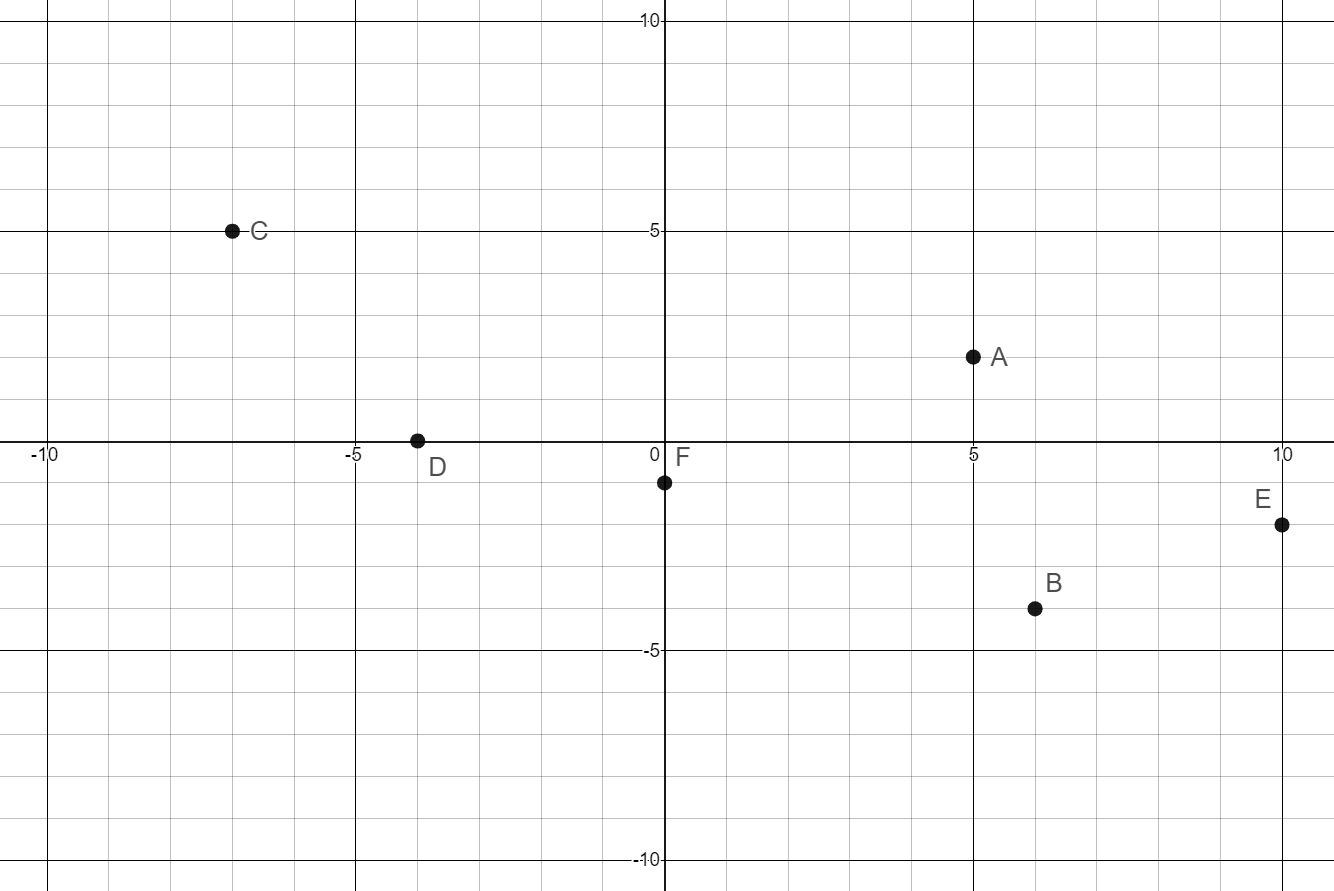  2. Coordinate plane graph with six points graphed. Point A is five units to the right of the origin and up two units. Point B is six units to the right of the origin and down four units. Point C is seven units to the left of the origin and up five units. Point D is four units to the left of the origin. Point E is ten units to the right of the origin and down two units. Point F is one unit down from the origin.

    Write the ordered pair for each point on the graph.
    • Point A

      • (5,2)

    • Point B

      • (6,-4)

    • Point C

      • (-7,5)

    • Point D

      • (-4,0)

    • Point E

      • (10,-2)

    • Point F

      • (0,-1)

    • Draw a line passing through points D and F

      • Line is decreasing from left to right. Line passes through points (-4,0) and (0,-1).

    • Name the y-intercept of this line.

      • Point F (0,-1)

    • Name the x-intercept of this line.

      • Point D (-4,0)


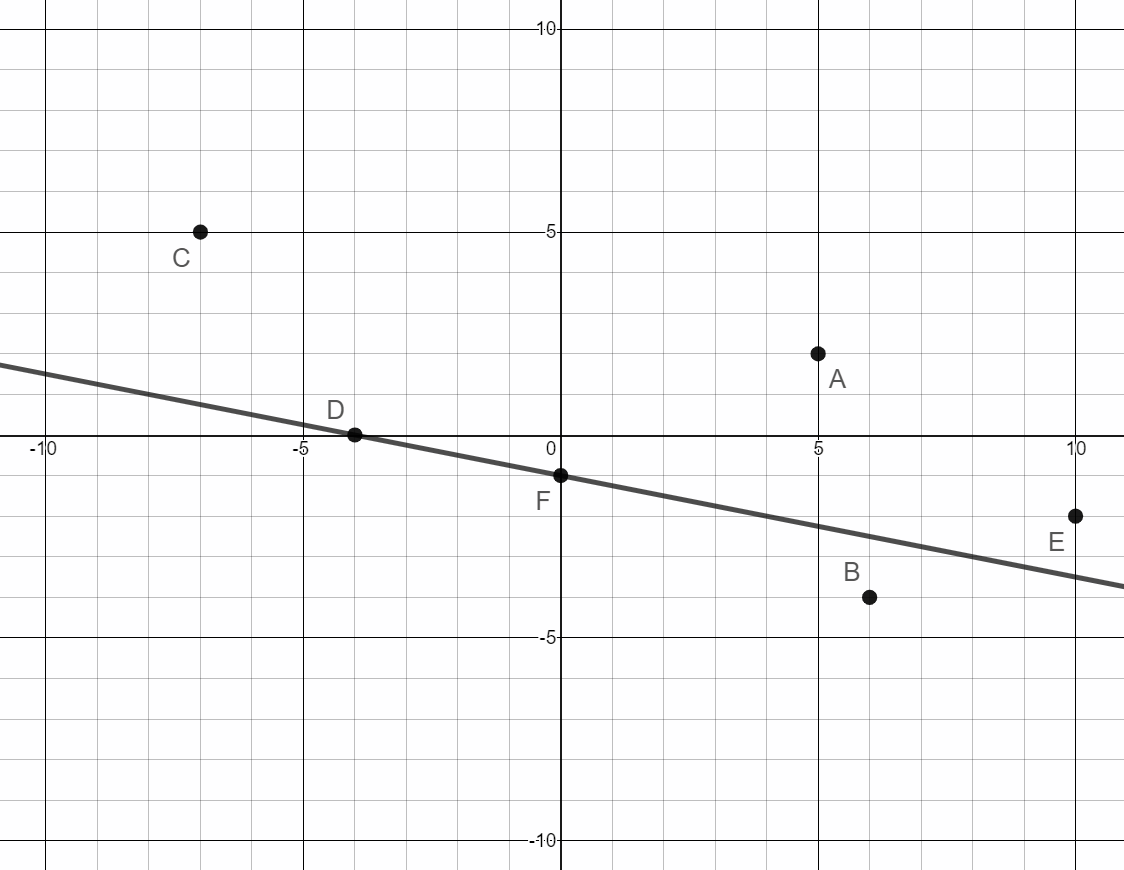
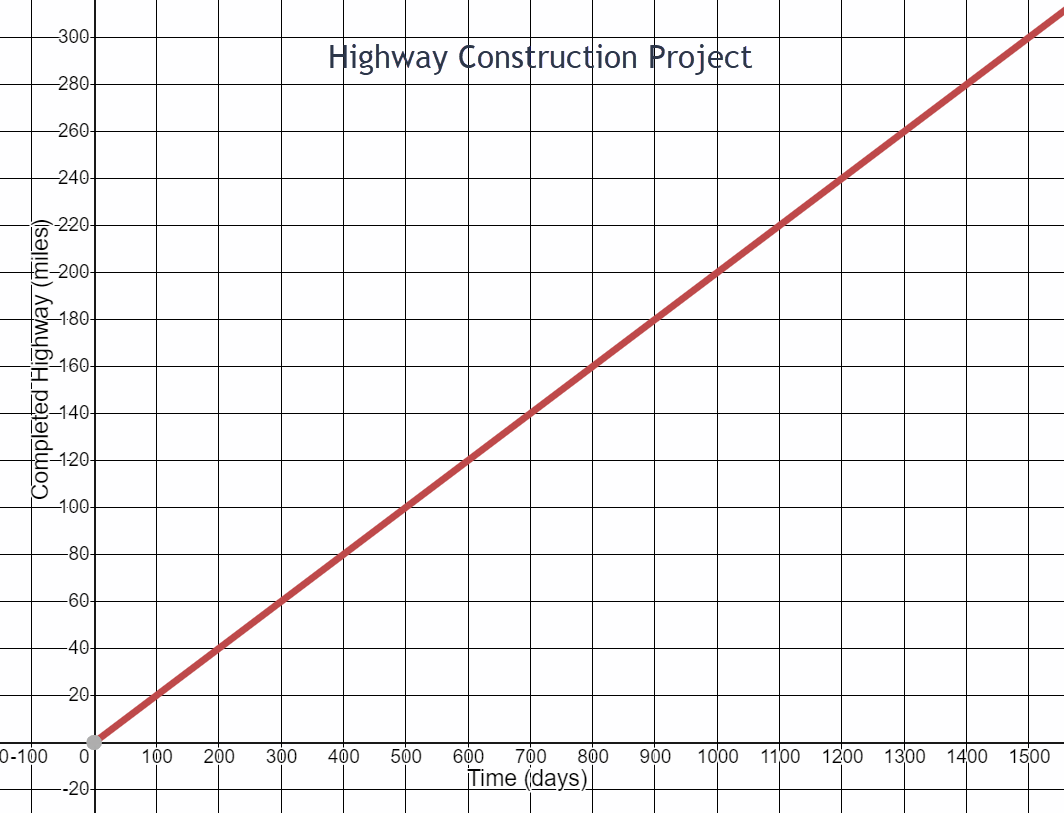
  3. Coordinate plane graph of Highway Construction Project. A line increasing from left to right is graphed. The horizontal axis for Time in days is numbered from zero to 1500 by hundreds. The vertical axis for Completed Highway miles is numbered from zero to 300 by twenties. The line starts at the point (0,0) and passes through points (100,20) and (1500,300).

    1. Consider the Highway Construction Project graph. How many miles had been completed at the beginning of the project? Write this as an ordered pair.

      2. zero miles (0,0)

    2. How many miles of highway were completed in 100 days? Write this as an ordered pair.

      3. 20 miles (100,20)

    3. What is the change in highway miles for each 100 days on the project? Write this rate of change as a fraction.

      4. \(\begin{equation}\frac{20\text{ miles}}{100\text{ days}}\end{equation}\)

    4. How many miles were completed in 5 days?

      5. 1 mile

    5. How many miles were completed in 1 day?

      6. 0.2 miles

    6. How many miles were completed in 300 days? Write this as an ordered pair.

      7. 60 miles (300,60)

    7. How much time did it take to complete 200 miles of highway? Write this as an ordered pair.

      8. 200 miles (1000,200)

    8. How many highway miles were completed between day 300 and day 1000 of the project?

      9. 140 miles

    9. What is the change in highway miles for each 700 days on the project? Write this rate of change as a fraction. Simplify your fraction.

      10. \(\begin{equation}\frac{140}{700}=\frac{1}{5}\text{ miles per day}\end{equation}\)


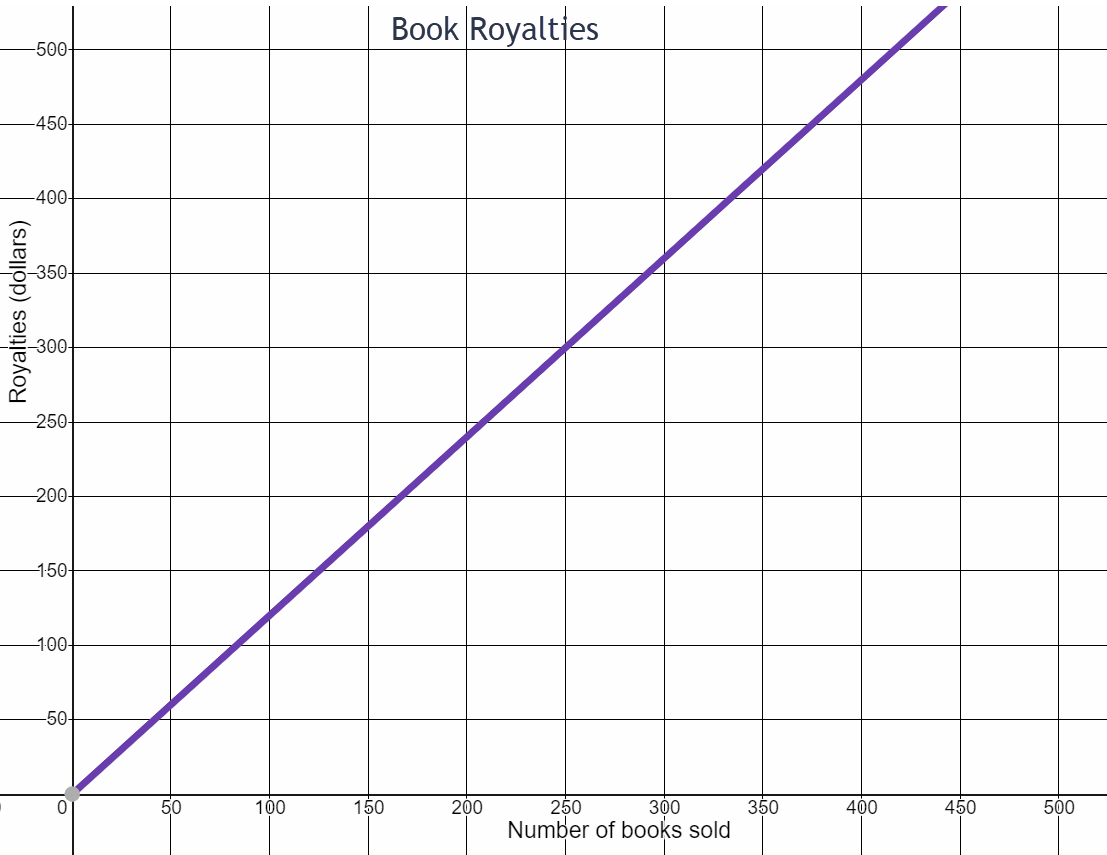
  4. Coordinate plane graph of Book Royalties. A line increasing from left to right is graphed. The horizontal axis for number of books sold is numbered from zero to 500 by fifties. The vertical axis for Royalties in dollars is numbered from zero to 500 by fifties. The line starts at the point (0,0) and passes through point (250,300).

    1. How much in royalties does the author receive for selling 0 books?

      2. $0

    2. How much in royalties does the author receive for selling 250 books?

      3. $300

    3. What is the rate of change in royalties for every 250 books sold? Write this rate of change as a fraction.

      4. \(\begin{equation} \frac{\$300}{250 \text{ books}} \end{equation}\)

    4. How much does the author receive in royalties for each book sold?

      5. $6 for 5 books which is $1.20 per book


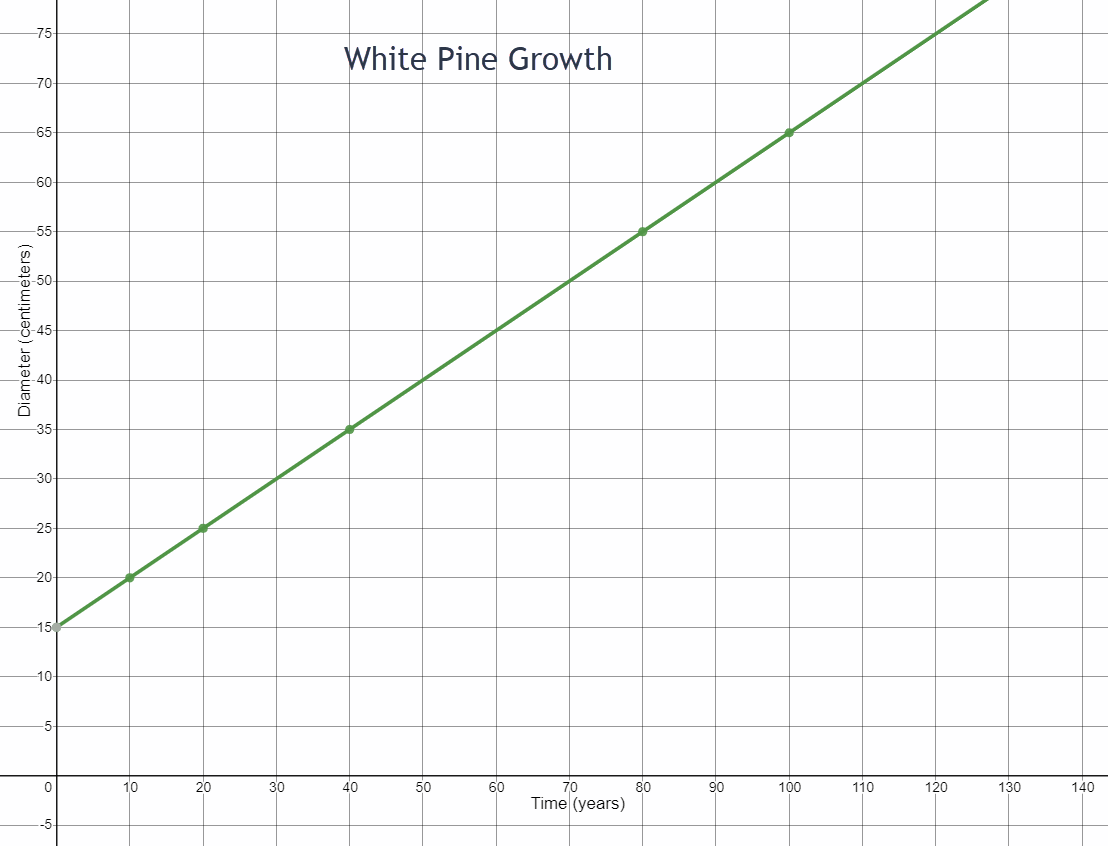
  5. Coordinate plane graph of White Pine Growth. A line increasing from left to right is graphed. The horizontal axis for time in years is numbered from zero to 140 by tens. The vertical axis for Diameter in centimeters is numbered from zero to 75 by fives. The line starts at the point (0,15) and passes through points (10,20) and (20,25) and (40,35) and (80,55) and (100,65).

    1. Write the ordered pairs for two points on the line.

      2. (40,35) (100,65) for example

    2. Find the change in diameter between your two points.

      3. \(\begin{equation}65-35=30\text{ cm}\end{equation}\)

    3. Find the change in time between your two points.

      4. \(\begin{equation}100-40=60\text{ years}\end{equation}\)

    4. Write the rate of change in centimeters per year as a fraction.

      5. \(\begin{equation}\frac{30\text{ cm}}{60\text{ years}}\end{equation}\)

    5. What was the initial diameter of the tree?

      6. 15 cm

    6. How fast did the tree grow?

      7. \(\begin{equation}\frac{1}{2}\text{ cm per year}\end{equation}\)


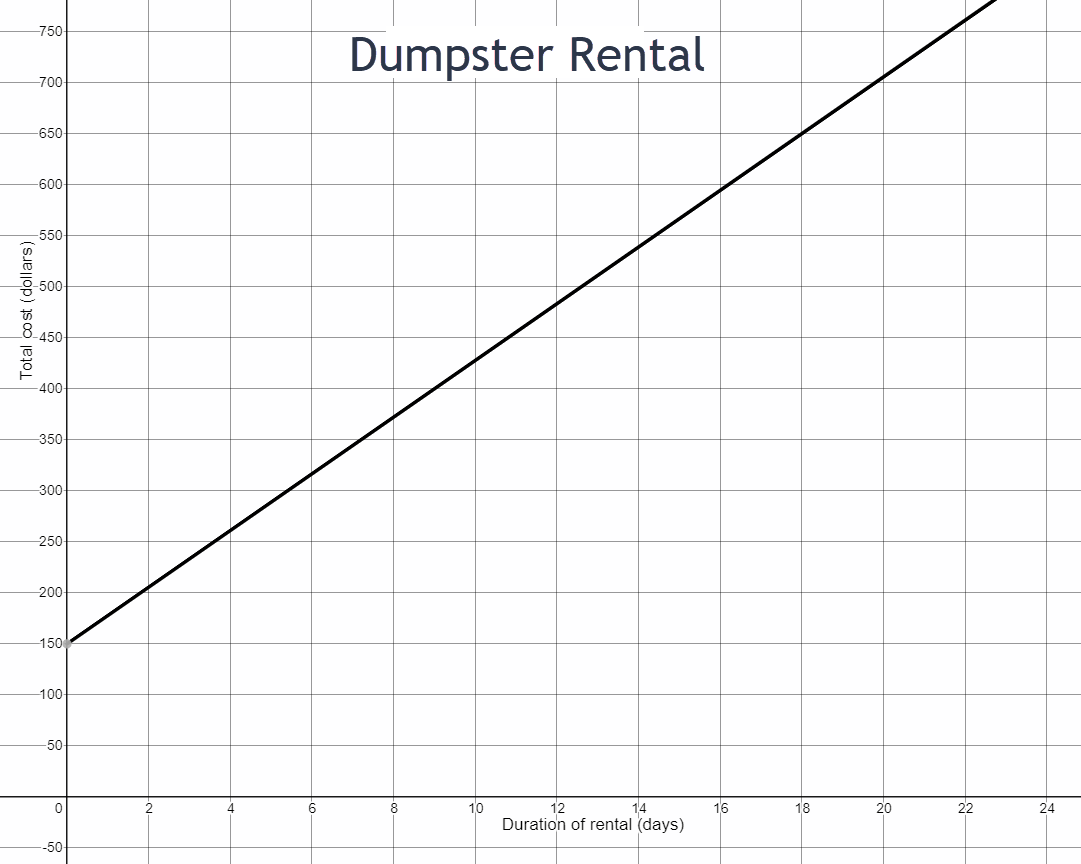
  6. Coordinate plane graph of Dumpstser Rental. A line increasing from left to right is graphed. The horizontal axis for Duration of Rental in days is numbered from zero to 24 by twos. The vertical axis for Total Cost in dollars is numbered from zero to 750 by fifties. The line starts at the point (0,150) and passes through point (18,650).

    1. What is the initial cost of the dumpster rental? Write this as an ordered pair.

      2. $150 (0,150)

    2. What is the total cost of the dumpster rental for 20 days? Write this as an ordered pair.

      3. $700 (20,700)

    3. Consider your two ordered pairs from parts a and b. What is the vertical change between these two points on the graph?

      4. \(\begin{equation}700-150=\$550\end{equation}\)

    4. What is the horizontal change between these two points on the graph?

      5. \(\begin{equation}20-0=20\text{ days}\end{equation}\)

    5. Write the rate of change as a fraction using your answers to parts c and d.

      6. \(\begin{equation}\frac{\$550}{20\text{ days}}\end{equation}\)

    6. Interpret this rate of change in context of the problem situation. Write a complete sentence.

      7. The cost of renting a dumpster is $27.50 per day.

  7. Two families are competing on a reality TV show. The goal of the show is to race from Los Angeles to New York. Each family is taking an indirect route and has different tasks to complete along the way. The family that completes the race in the least amount of time wins.

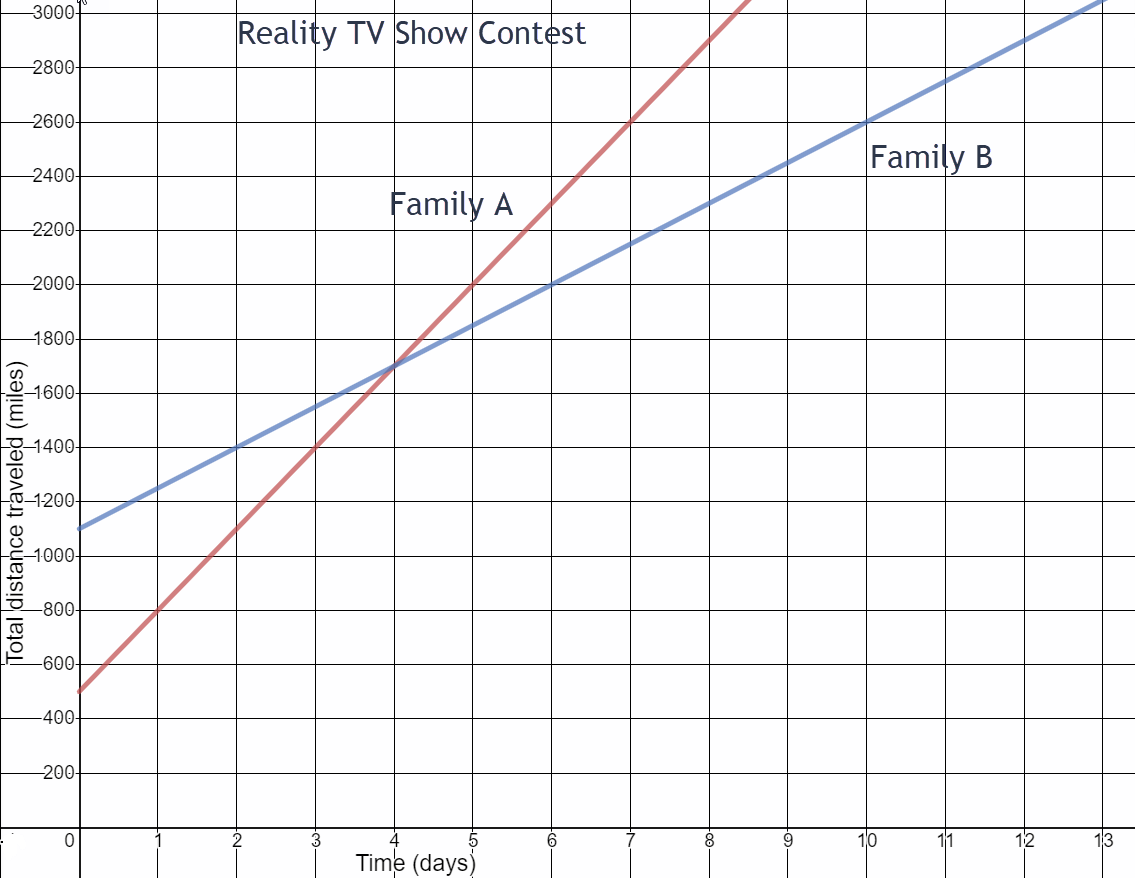
    Coordinate plane graph of Reality TV Show Contest. The graph shows two lines increasing from left to right. The horizontal axis for Time in days is numbered from zero to 13 by ones. The vertical axis for Total distance traveled in miles is numbered from zero to 3000 by two hundreds. Line A starts at the point (0,500) and passes through point (5,2000). Line B starts at the point (0,1100) and passes through points (2,1400) and (6,2000).

    1. How many miles did Family A complete in the race before now?

      2. 500 miles

    2. How many miles did Family B complete in the race before now?

      3. 1100 miles

    3. What is Family A’s speed?

      4. \(\begin{equation}\text{ Family A: }\frac{2000-500}{5-0}=300\end{equation}\)

      300 miles per day

    4. What is Family B’s speed?

      5. \(\begin{equation}\text{ Family B: }\frac{2000-1100}{6-0}=150\end{equation}\)

      150 miles per day

    5. Who appears to be winning the race?

      6. Family A

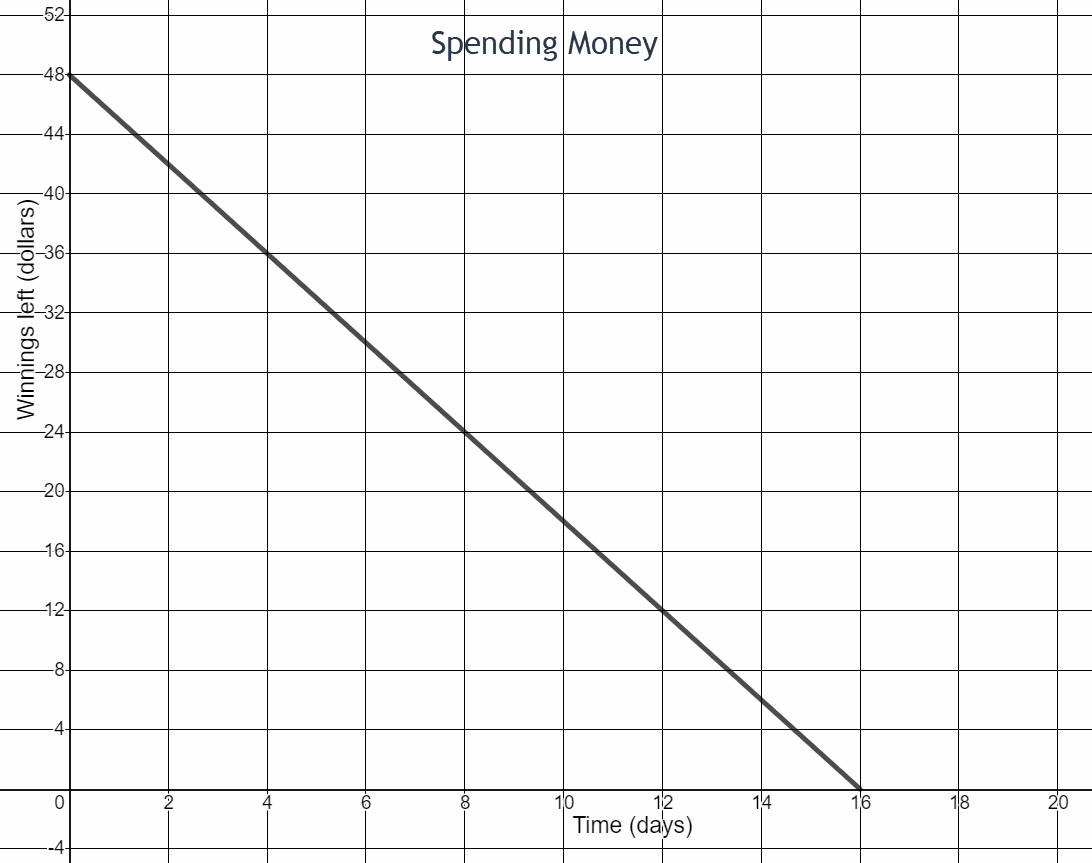
  8. You won a Ping Pong tournament. Now you are monitoring your spending.Coordinate plane graph of Spending Money. A line decreasing from left to right is graphed. The horizontal axis for Time in days is numbered from zero to 20 by twos. The vertical axis for Winnings Left in dollars is numbered from zero to 52 by fours. The line starts at the point (0,48) and passes through point (8,24) and ends at point (16,0).

    1. How much money did you win in the tournament?

      2. $48

    2. Write the ordered pairs for two points on this line.

      3. (0,48) and (16,0)

    3. Write the slope of the line as a fraction. What part of the fraction indicates that the line in the graph is decreasing?

      4. \(\begin{equation}\frac{-48}{16}=\frac{-3}{1}\end{equation}\)

      The negative sign indicates the line is decreasing.

    4. Interpret the slope in the context of the scenario. Write a complete sentence.

      5. You spend $3 per day.

  9. Here’s a different scenario for monitoring your spending after winning the Ping Pong tournament.
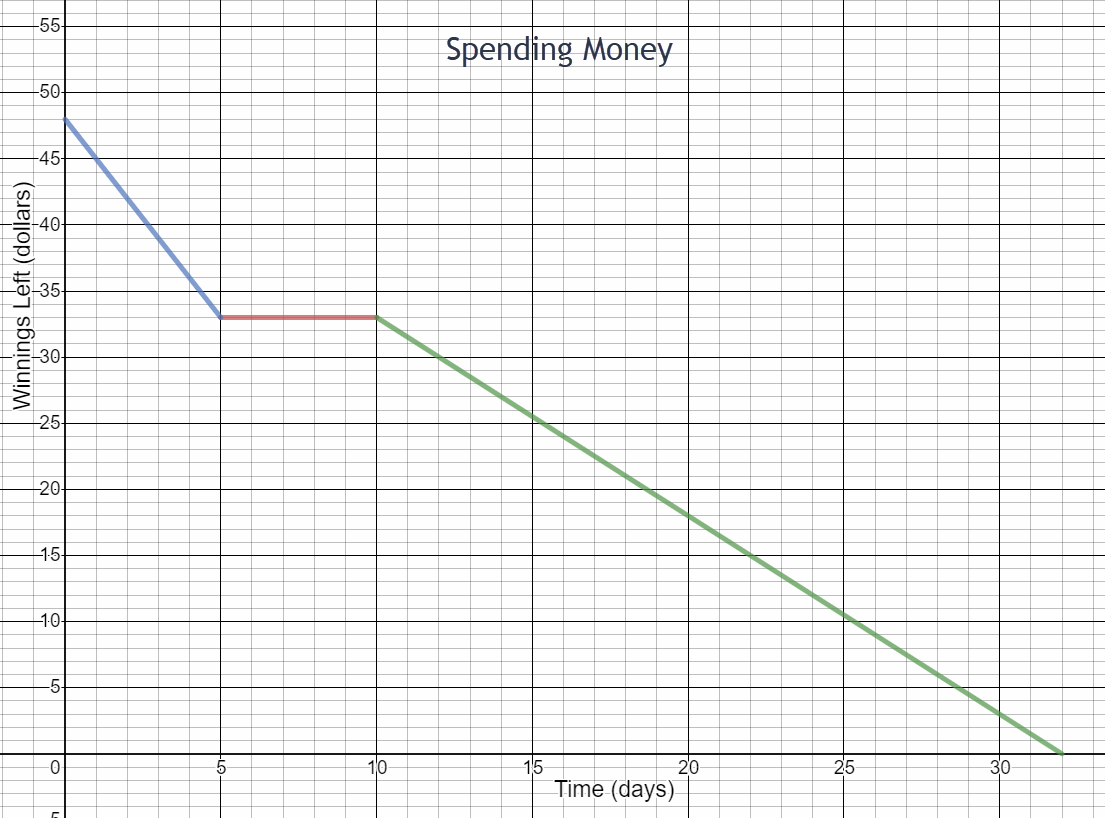
    Coordinate plane graph of Spending Money. The horizontal axis for Time in days is numbered from zero to 35 by fives. The vertical axis for Winnings Left in dollars is numbered from zero to 55 by fives.A line segment decreasing from left to right starts at (0,48) and ends at (5,33). A horizontal line segment starts at (5,33) and ends at (10,33). Another line segment starts at (10,33) and ends at (32,0).

    1. How much did you spend in the first five days after the tournament?

      2. \(\begin{equation}48-33=\$15\end{equation}\)

    2. How much did you spend per day in the first five days after the tournament?

      3. $3 per day

    3. What does the segment between 5 and 10 days represent?

      4. You did not spend any money.

    4. How much did you spend between day 10 and day 32? What is the rate of change for this time period?

      5. \(\begin{equation}\frac{\$33}{22\text{ days}}=\$1.50\text{ per day}\end{equation}\)

    5. When did you spend money at the fastest rate according to this graph?

      6. Days 1 through 5