Statistics Unit

2.10 The Normal Distribution

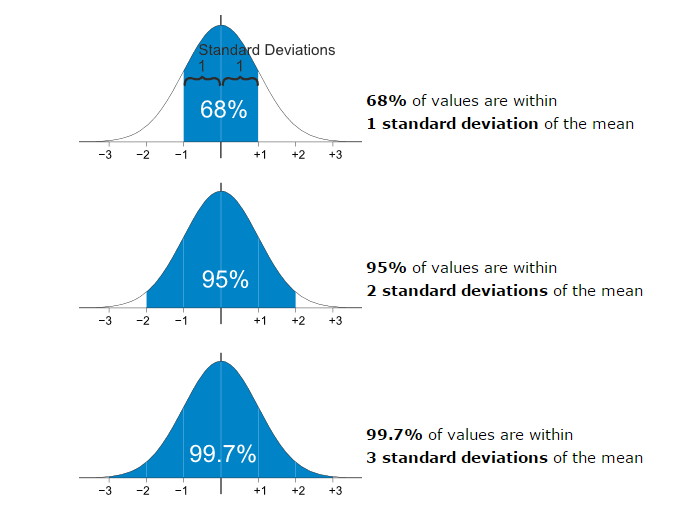
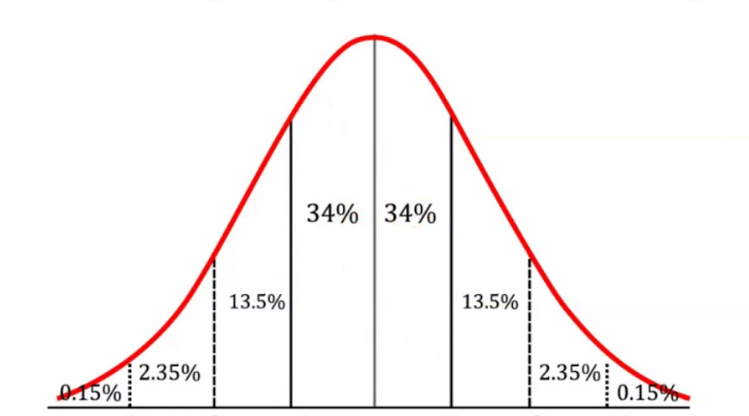
The normal distribution is the most commonly-used probability distribution in all of statistics.

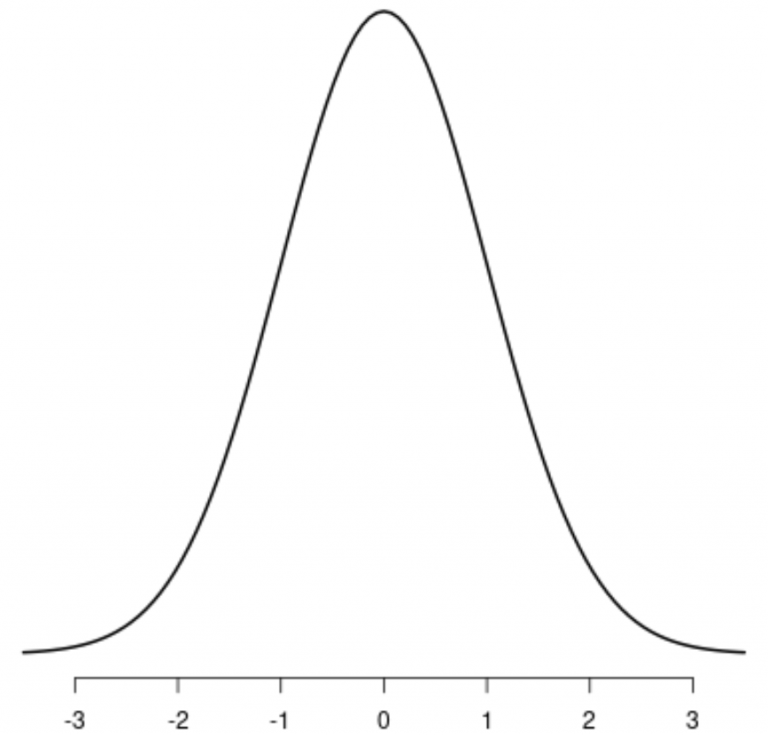
A graph of a normal curve. The number line below the curve is numbered from -3 to 3 counting by 1. The graph is close to the number line on the left side of -3 and rises to a peak at 0 then goes back down close to the number line past 3.



It has the following properties:

Examples of things that are normally distributed.

source https://www.statology.org/example-of-normal-distribution/

There are three graphs in the picture. All three graphs are of the same bell-shaped curve, a normal distribution curve. The x-axis shows the mean in the middle, the highest point of the graph. Three standard deviations to the left and to the right are also marked on the graph. So, the x-axis reads, -3, -2, -1, mean, +1, +2, +3. The first graph is shaded below the curve between -1 and +1 to show that 68% of all data in a normal distribution will be between -1 and +1 standard deviations from the mean. The second graph is shaded below the curve from -2 to +2 to show that 95% of the data in a normal distribution is between -2 and +2 standard deviations from the mean. The third graph is shaded below the curve from -3 to +3 to show that 99.7% of the data in a nomral distribution is between -3 and +3 standard deviations from the mean.

The graph is a normal distribution curve very similar to the previous graphs. On this graph, percentages of data are shown between each standard deviation mark on the x-axis. The percentage between -3 and -2 is 2.35%. The percentage between -2 and -1 is 13.5%. The percentage between -1 and the mean is 34%. The percentage between the mean and +1 is 34%. The percentage between +1 and +2 is 13.5%. The percentage between +2 and +3 is 2.35%. These percentages represent the percent of data that lies between each of the standard deviations. For example, 13.5% of all data in a normal distribution are between -2 and -1 standard deviations from the mean.

  1. The amount of Coca-Cola in a two-liter bottle is normally distributed with a mean of 2.05 liters and a standard deviation of 0.1 liters. (0.1 liters is approximately 3 ounces or 0.4 cups)

    Sketch a distribution curve and label.

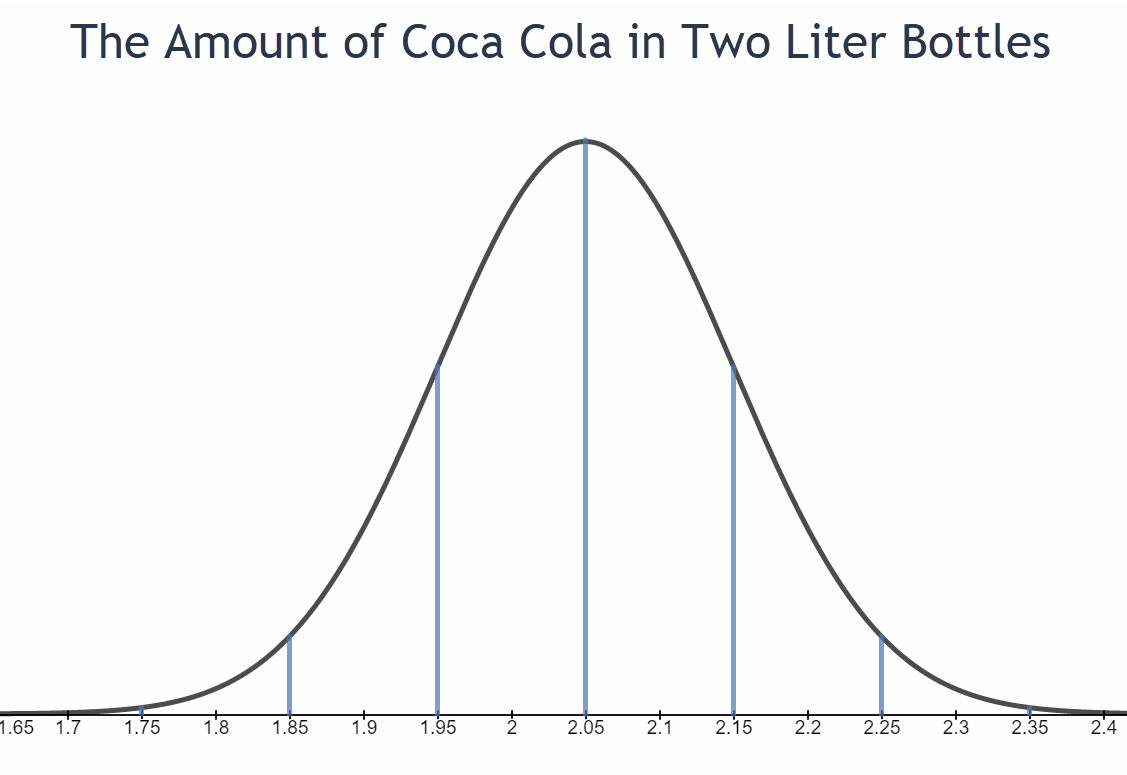
    The graph is a bell-shaped curve. The x-axis is labeled with the mean in the middle, the highest point of the curve. Three standard deviations to the left and three standard deviations to the right are labeled on the x-axis. So, the x-axis contains 1.75, 1.85, 1.95, 2.05, 2.15, 2.25, and 2.35.

    1. What percentage of two-liter Coca-Cola bottles contain between 1.95 and 2.15 liters?

      2. 68%

    2. What percentage of two-liter Coca-Cola bottles contain more than 2.05 liters?

      3. 50%

    3. The range of liters that approximately 95% of all Coca-Cola bottles is from ___________ to ___________.

      4. 1.85 to 2.25 liters

    4. What percentage of two-liter bottles contain between 1.85 and 2.15 liters?

      5. 81.5%

    5. What percentage of two-liter bottles contain less than 1.85 liters?

      6. 2.5%

    6. In a sample of 10,000 two-liter Coca-Cola bottles, how many would be expected to contain more than 2.35 liters? (This is almost 1.5 cups above the advertised 2 liters)

      7. \(.0015 \cdot 10000 = 15\) bottles

  2. The average gas mileage for a hybrid Honda Civic is normally distributed with a mean of 44 miles per gallon and a standard deviation of 5 mpg.

    Sketch a distribution curve and label.

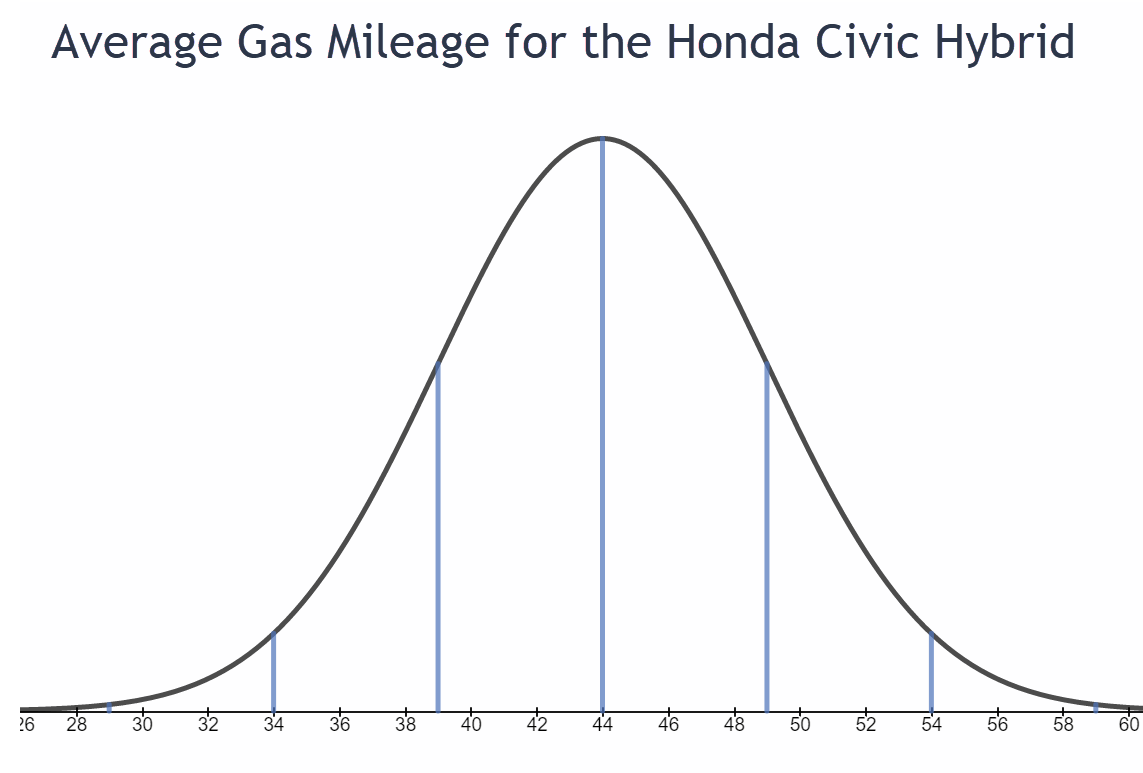
    The graph is a bell-shaped curve. The x-axis is labeled with the mean in the middle, the highest point of the curve. Three standard deviations to the left and three standard deviations to the right are labeled on the x-axis. So, the x-axis contains 29, 34, 39, 44, 49, 54, and 59.

    1. What percentage of Honda Civic hybrids get better than an average of 49 miles per gallon?

      2. 16%

    2. What percentage of Civic hybrids get worse than an average of 39 miles per gallon?

      3. 16%

    3. What percentage of Civic hybrids get between 29 and 39 miles per gallon?

      4. 15.85%

    4. The range in miles per gallon for 99.7% of Civic Hybrids is from ______________ to ______________.

      5. 29 to 59 mpg

    5. In a sample of 500 Civic hybrids, how many would be expected to get between 39 and 49 miles per gallon on average?

      6. \(0.68 \cdot 500 = 340\) Honda Civic Hybrids

    6. In a sample of 500 Civic hybrids, how many would be expected to get better than an average of 59 miles per gallon?

      7. \(0.0015 \cdot 500 = 0.75\)

      Less than one Honda Civic Hybrid per 500 Civics will get between 39 and 49 mpg.