Statistics Unit

2.7 Measures of Central Tendency (Mean/Median/Mode/Midrange)

Find the mean, median, and midrange for each of these data sets:

  1. 1,1,2,2,7,9,9,9,9

    2. Mean: 5.4

    Median: 7

    Midrange: 5

  2. 6,6,7,7,7,7,8,8,9

    3. Mean: 7.2

    Median: 7

    Midrange: 7.5

  3. 1,4,8,8,8,9,9,9,9

    4. Mean: 7.2

    Median: 8

    Midrange: 5

  4. Which of these data sets have the same mean? same median? same midrange?

    5. #2 and #3 have the same mean.

    #1 and #2 have the same median.

    #1 and #3 have the same midrange.

  5. If each data set represents a class set of quiz scores, which class did the best on the quiz? How do you know?

    6. The class in #3 did the best on the quiz because the median score is the highest of the three data sets.

Which of these data sets have the same median? Same mean? Same midrange?

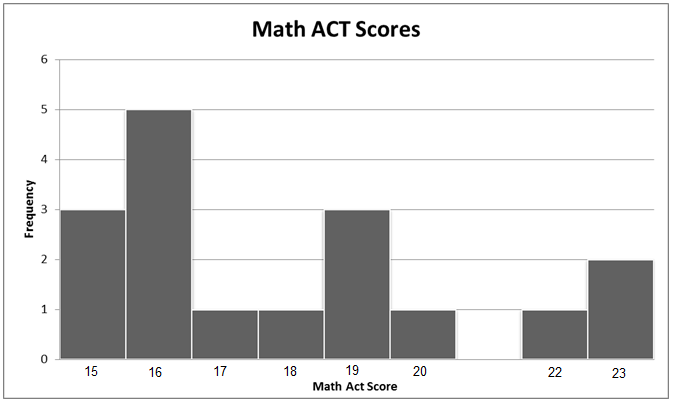
The graph is a bar graph depicting the ACT math scores for students in one MATH 1010 class. The x-axis represents the score and ranges from 15 to 23. The y-axis represents the number of students who had the given score. There were 3 students with a 15, 5 students who scored a 16, 1 student who scored a 17, 1 student who scored an 18, 3 students who scored a 19, 1 student who scored a 20, no students scoring a 21, 1 student who scored a 22, and 2 students who scored a 23.
  1. Find the average (mean) math ACT score of the class.

    2. \( \begin{equation} \frac{(15 \times 3)+(16 \times 5)+(17 \times 1)+(18 \times 1)+(19 \times 3)+(20 \times 1)+(22 \times 1)+(23 \times 2)}{3+5+1+1+3+1+1+2}= \frac{305}{17}=17.9 \end{equation} \)

  2. Find the median math ACT score of the class.

    3. 17

  3. Find the midrange of the math ACT scores of the class.

    4. 19

  4. Identify the mode of the math ACT scores of the class.

    5. 16

  5. Suppose a new student joined the class. The student’s math ACT score was a 35. How does this affect the mean, median, and midrange?

    6. Mean: 18.9

    Median: 17.5

    Midrange: 25