MATH 1830

4.5 Area between Curves

Introduction

Before 1995, the U. S. Census Bureau used the model below to project the number (in thousands) of households in the United States, where $t$ is the number of years after 1990. $${N_1} = 1.35{t^2} + 1078.4t + 92,323\quad$$ For the years 1995-2005, the actual number of households $N$ in the United States can be modeled by $${N_2} = 18.32{t^2} + 1178.3t + 92,099$$

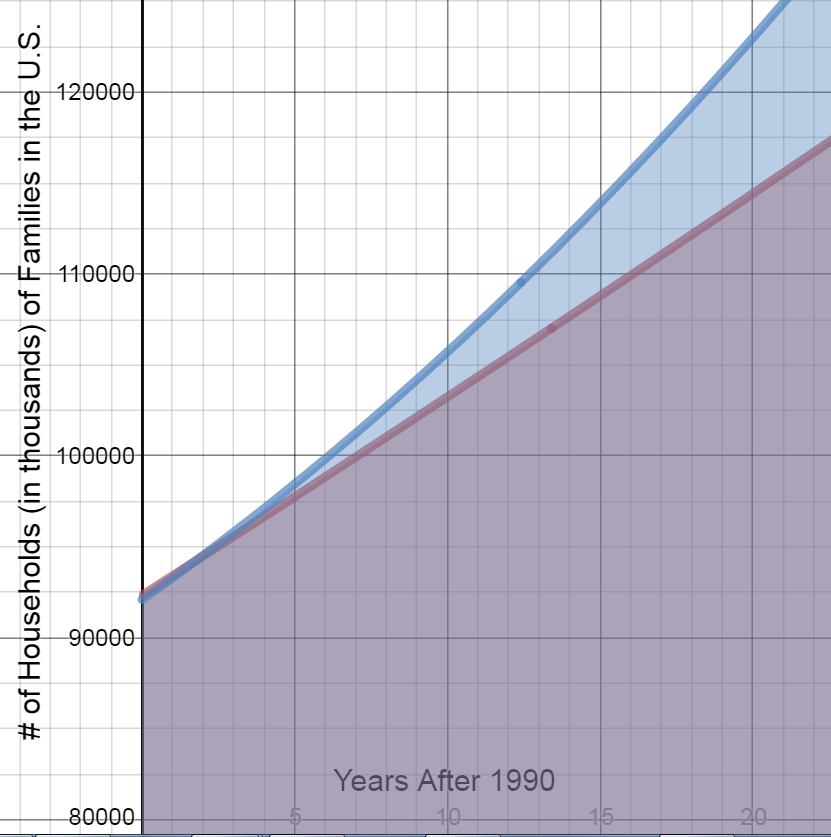
1. Graph ${N_1}$ on the interval $\;5 \le t \le 15$ and shade the area under the curve. What does this shaded area represent?

   This shaded area represents the projected number of households in the United States from 1995 to 2005.

   

   

2. Now graph ${N_2}$ on the interval $\;5 \le t \le 15$ on the same graph and shade the area under the curve. What does this shaded area represent? 

   This shaded area represents the actual number of households in the United States from 1995 to 2005.

3. Did the projection model over-project or under-project the number of households?

   The projection model under-projected the number of households.

4. How would you determine the difference in the number of households given by each model?

   Subtract the bottom equation from the top.

5. Find the difference in the number of households for the two models.  

   $\begin{align}&\int_{5}^{15}{\left((18.32{{x}^{2}}+1178.3x+92,099)-(1.35{{x}^{2}}+1078.4x+92,323)\right)\;dx}\end{align}$

   $=26,134.17$

   The difference between the two models is 26,134 households.

4.5 Video

Find the area bounded by the graphs of the indicated equations. Compute answers to three decimal places.

1. $y_1 = {x^3} + 1 \quad$ and $\quad y_2 = x + 1$

   

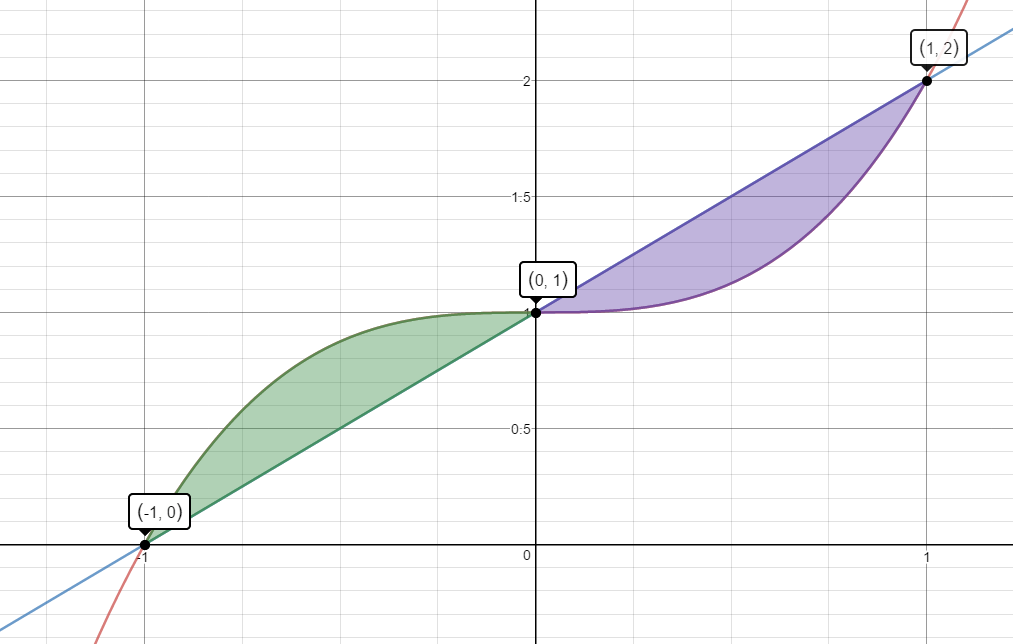
   $Area=\begin{align}&\int_{-1}^{0}\left(y_1-y_2\right)\;dx\end{align}$$+\begin{align}&\int_{0}^{1}\left(y_2-y_1\right)\;dx\end{align}$

   $\begin{align}&\int_{-1}^{0}\left(({{x}^{3}}+1)-(x+1)\right)\;dx\end{align}$$+\begin{align}&\int_{0}^{1}\left((x+1)-({{x}^{3}}+1)\right)\;dx\end{align}$

   $\begin{align}&\int_{-1}^{0}{({{x}^{3}}-x)\;dx}\end{align}$$+\begin{align}&\int_{0}^{1}{(x-{{x}^{3}})\;dx}\end{align}$

   $(\frac{{x}^{4}}{4}-\frac{{x}^{2}}{2})|_{-1}^{0}+(\frac{{x}^{2}}{2}-\frac{{x}^{4}}{4})|_{0}^{1}$

   $[(0-0)-(\frac{1}{4}-\frac{1}{2})]+[(\frac{1}{2}-\frac{1}{4})-(0-0)]$

   $\frac{1}{4}+\frac{1}{4}$

   $\frac{1}{2}\;units^2$

4.5 Lecture

2. $y_1 = \; - x + 7$ and $y_2 = 0$ on the interval $ - 3 \le x \le 3$

   $Area=\begin{align}&\int_{-3}^{3}{\left(y_1-y_2 \right) dx}\end{align}$

   $=\begin{align}&\int_{-3}^{3}{\left((-x+7)-0 \right) dx}\end{align}$

   $=\left(-\frac{{{x}^{2}}}{2}+7x+C\right)│ _{-3}^{3} $

   $=(-\frac{9}{2}+21+C)-(-\frac{9}{2}-21+C)$

   $=-\frac{9}{2}+21+C+\frac{9}{2}+21-C$

   $=42\ unit{{s}^{2}}$

3. $y_1 = \; - x - 3\quad$ and $\quad y_2 = 0\quad$ on the interval $ - 7 \le x \le 2$

   $Area=\begin{align}&\int_{-7}^{-3}\left(y_1-y_2\right)\;dx\end{align}$$+\begin{align}&\int_{-3}^{2}\left(y_2-y_1\right)\;dx\end{align}$

   $=\begin{align}&\int_{-7}^{-3}\left(\left(-x-3\right)-0\right)\;dx\end{align}$$+\begin{align}&\int_{-3}^{2}\left(0-\left(-x-3\;\right)\right)\;dx\end{align}$

   $=\left(-\frac{x^2}2-3x+C\right)|_{-7}^{-3}+\left(\frac{x^2}2+3x+C\right)|_{-3}^2$

   $=(4.5--3.5)+(8--4.5)$

   $=8+12.5$

   $=20.5\ unit{{s}^{2}}$

4.5 Group Work

4. $y_1 = \; - \frac{1}{4}{x^3} + 2 \quad$ and $\quad y_2 = 0 \quad$ on the interval $ - 2 \le x \le 1$

   $Area=\begin{align}&\int_{-2}^{1}{\left(y_1-y_2 \right) dx}\end{align}$

   $=\begin{align}&\int_{-2}^{1}{\left(\left(-\frac{1}{4}{{x}^{3}}+2\right)-0 \right) dx}\end{align}$

   $=\left(-\frac{1}{4}\left(\frac{{{x}^{4}}}{4}\right)+2x+C \right)\left)│ _{-2}^{1} \right.$

   $=(-\frac{{{x}^{4}}}{16}+2x+C\left)│ _{-2}^{1} \right.$

   $=(-\frac{1}{16}+2+C)-(-\frac{16}{16}-4+C)$

   $=-\frac{1}{16}+2+1+4$

   $=6.9375\ unit{{s}^{2}}$

5. $y_1 = \;x\left( {4 + x} \right)\quad $ and $\quad y_2 = 0 \quad$ on the interval $\; - 3 \le x \le - 1$

   $Area=\begin{align}&\int_{-3}^{-1}{\left(y_2-y_1 \right) dx }\end{align}$

   $=\begin{align}&\int_{-3}^{-1}{\left(0-(4x+{{x}^{2}})\right)\;dx}\end{align}$

   $=\begin{align}&\int_{-3}^{-1}{\left(-4x-{{x}^{2}} \right)}\;dx\end{align}$

   $=(-\frac{4{{x}^{2}}}{2}-\frac{{{x}^{3}}}{3}+C\left)│ _{-3}^{-1} \right.$

   $=(-2{{x}^{2}}-\frac{{{x}^{3}}}{3}+C\left)│ _{-3}^{-1} \right.$

   $=(-2(1)-(-\frac{1}{3})+C)-(-2(9)-(-9)+C)$

   $=-2+\frac{1}{3}+18-9$

   $=7.33\ unit{{s}^{2}}$

6. $y_1 = \; - \frac{2}{x}\quad$ and $\quad y_2 = 0 \quad$ on the interval $1 \le x \le e$

   $Area=\begin{align}&\int_{1}^{e}{\left(y_2-y_1 \right) dx }\end{align}$

   $=\begin{align}&\int_{1}^{e}{\left(0-(-\frac{2}{x})\right)\; dx}\end{align}$

   $=\begin{align}&\int_{1}^{e}{\frac{2}{x}}\; dx\end{align}$

   $=(2\ln \left| x \right|+C\left)│ _{1}^{e} \right.$

   $=2\ln e-2\ln 1$

   $=2(1)-2(0)$

   $=2\ unit{{s}^{2}}$

7. $y_1 = \; - x + 7\quad$ and $\quad y_2 = - 2\quad$ on the interval $ - 3 \le x \le 3$

   $Area=\begin{align}&\int_{-3}^{3}{(y_1-y_2)\;dx}\end{align}$

   $=\begin{align}&\int_{-3}^{3}{\left((-x+7)-(-2)\right)\;dx}\end{align}$

   $=\begin{align}&\int_{-3}^{3}{\left(-x+7+2\right)\;dx}\end{align}$

   $=\begin{align}&\int_{-3}^{3}{\left(-x+9\right)\;dx}\end{align}$

   $=(-\frac{{{x}^{2}}}{2}+9x+C\left)│ _{-3}^{3} \right.$

   $=(-\frac{9}{2}+27+C)-(-\frac{9}{2}-27+C)$

   $=-\frac{9}{2}+27+C+\frac{9}{2}+27-C$

   $=54\ unit{{s}^{2}}$

8. $y_1 = \; - x - 3 \quad$ and $\quad y_2 = 1.5\quad$ for the interval $ - 7 \le x \le 2$

   $Area=\begin{align}&\int_{-7}^{-4.5}\left(y_1-y_2\right)\;dx\end{align}$$+\begin{align}&\int_{-4.5}^{2}\left(y_2-y_1\right)\;dx\end{align}$

   $\begin{align}&\int_{-7}^{-4.5}\left(\left(-x-3\right)-1.5\right)\;dx\end{align}$$+\begin{align}&\int_{-4.5}^{2}\left(1.5-\left(-x-3\;\right)\right)\;dx\end{align}$

   $\begin{align}&\int_{-7}^{-4.5}\left(-x-4.5\right)\;dx\end{align}$$+\begin{align}&\int_{-4.5}^{2}\left(4.5+x\right)\;dx\end{align}$

   $(\frac{-{{x}^{2}}}{2}-4.5x+C\left)│ _{-7}^{-4.5} \right.$

   $+(4.5x+\frac{{{x}^{2}}}{2}+C\left)│ _{-4.5}^{2} \right.$

   $(10.125-7)+(11--10.125)$

   $3.125+21.125$

   $24.25\ unit{{s}^{2}}$

9. $y_1 = \;\ln (x + e) \quad$ and $\quad y_2 = {e^x} - 5\quad$ on the interval $0 \le x \le 1$

   $Area=\begin{align}&\int_{0}^{1}\left(y_1-y_2\right)\;dx\end{align}$

   $=\begin{align}&\int_{0}^{1}\left(\ln (x+e)-({{e}^{x}}-5)\right)\;dx\end{align}$

   $=\begin{align}&\int_{0}^{1}\left(\ln (x+e)-{{e}^{x}}+5\right)\; dx\end{align}$

   $=\begin{align}&\int_{0}^{1}\ln (x+e)\; dx\end{align}$$+\begin{align}&\int_{0}^{1}\left(-{{e}^{x}}+5\right)\; dx\end{align}$

   $u=x+e$

   $du=dx$

   $=\begin{align}&\int_{x=0}^{x=1}ln u\;du +\int_{0}^{1}(-{{e}^{x}}+5)\;dx\end{align}$

   $=\left(u\ln\left|u\right|-u+C\right)\vert_{x=0}^{x=1}+\left(-e^x+5x\right)|_0^1$

   $=\left[\left(x+e\right)\ln\left|x+e\right|-\left(x+e\right)+-e^x+5x\right]|_0^1$

   $=((1+e)\ln \left| 1+e \right|-1-e-e+5)-((0+e)\ln \left| 0+e \right|-0-e-{{e}^{0}}+0)$

   =$3.45-(e\ln e-e-1)$

   =$3.45-(-1)$

   =$4.45\;units^2$

   Define the total area bounded by the two functions. How would you determine the interval, if you were asked to calculate the total area bounded between the two functions?

   Area Not Bounded by an Interval

   Find the area bounded by the graphs of the indicated equations.

10. $y_1 = - {x^3} - 2{x^2} + 1\quad$ and $\quad y_2 = - x - 1$

    $Area=\begin{align}&\int_{-2}^{-1}\left(y_2-y_1\right)\;dx\end{align}$$+\begin{align}&\int_{-1}^{1}\left(y_1-y_2\right)\;dx\end{align}$

    $\begin{align}&\int_{-2}^{-1}\left((-x-1)-(-{{x}^{3}}-2{{x}^{2}}+1)\right)\;dx\end{align}$$+\begin{align}&\int_{-1}^{1}\left((-{{x}^{3}}-2{{x}^{2}}+1)-(-x-1)\right)\;dx\end{align}$

    $\begin{align}&\int_{-2}^{-1}\left(-x-1+x^3+2x^2-1\right)\;dx+\int_{-1}^1\left(-x^3-2x^2+1+x+1\right)\;dx\end{align}$

    $\begin{align}&\int_{-2}^{-1}\left(x^3+2x^2-x-2\right)\;dx+\int_{-1}^{1}\left(-x^3-2x^2+x+2\right)\ dx\end{align}$

    $(\frac{{{x}^{4}}}{4}+\frac{2{{x}^{3}}}{3}-\frac{{{x}^{2}}}{2}-2x+C\left)| _{-2}^{-1} \right.+(\frac{-{{x}^{4}}}{4}-\frac{2{{x}^{3}}}{3}+\frac{{{x}^{2}}}{2}+2x+C\left)| _{-1}^{1} \right.$

    $(1.0833-0.667)+(1.5833--1.0833)$

    $0.4167+2.6667$

    $3.08\;units^2$

11. $y_1 = - 3 + {x^2}$ and $y_2 = - {e^{2x - 3}} + 2$

    The functions intersect at $x=1.79$ and $x=-2.24$, therefore the area is bound in the interval [-2.24, 1.79].

    Area=$\begin{align}&\int_{-2.24}^{1.79}(y_2-y_1)\;dx\end{align}$

    $=\begin{align}&\int_{-2.24}^{1.79}{(-{{e}^{2x-3}}+2)-(-3+{{x}^{2}}})\;dx\end{align}$

    $=\begin{align}&\int_{-2.24}^{1.79}\left(-e^{2x-3}-x^2+5\right)\;dx\end{align}$

    $u=2x-3$

    $du=2dx$

    $=\frac{1}{2}\begin{align}&\int_{x=-2.24}^{x=1.76}{-{{e}^{u}}\;du}+\int_{-2.24}^{1.76}{-{{x}^{2}}+5\; dx}\end{align}$

    $=\frac{1}{2}(-{{e}^{u}})\left| _{x=-2.24}^{x=1.79} \right.+(\frac{-{{x}^{3}}}{3}+5x\left)| _{-2.24}^{1.79} \right.$

    $=(\frac{-{{e}^{2x-3}}}{2}-\frac{{{x}^{3}}}{3}+5x\left)| _{-2.24}^{1.79} \right.$

    $=6.15-(-7.45)$

    $=13.6\;units^2$

12. The useful life of a piece of rental equipment is the duration for which the equipment will be profitable to the rental business, and not how long the equipment will actually last. Many factors affect a piece of equipment’s useful life, including the frequency of use, the age when acquired and the repair policy and certain environmental conditions. The change in revenue for renting the equipment, over time, is modeled by $$R'\left( t \right) = 4t{e^{ - 0.2{t^2}}},$$ in thousands of dollars per year. The change in cost for routine maintenance of the equipment is modeled by $$C'\left( t \right) = .5t,$$ also in thousands of dollars per year. Find the area between the graphs of $C'$ and $R'$ over the interval from the time the equipment is purchased until the equipment reaches the end of its useful life. Interpret the results.

    Note: The end of the useful life is t where $C'\left( t \right) = R'(t)$.

    Area =$\begin{align}&\int_{0}^{3.22}R'(t)-C'(t)\;dt\end{align}$

    $=\begin{align}&\int_{0}^{3.22}{(4t{{e}^{-0.2{{t}^{2}}}}-0.5t})\;dt\end{align}$

    $u=-0.2{{t}^{2}}$

    $du=-0.4t\;dt$

    $=\frac{4}{-0.4}\begin{align}&\int_{t=0}^{t=3.22}{e^u}\;du+\int_{0}^{3.22}-0.5t\;dt\end{align}$

    $=-10\begin{align}&\int_{t=0}^{t=3.22}{{{e}^{u}}}\;du +\int_0^{3.22}-0.5t\;dt\end{align}$

    $=-10{{e}^{u}}\left| _{t=0}^{t=3.22} \right.+\frac{-0.5{{t}^{2}}}{2}\left| _{0}^{3.22} \right.$

    $=-10{{e}^{-0.2{{t}^{2}}}}-0.25{{t}^{2}}\left| _{0}^{3.22} \right.$

    $=-3.85-(-10)$

    $=6.15$

    The useful life of this piece of equipment is 6.15 years.

4.5 Additional Practice

Find the area bounded by the graphs of the given equations over the given interval. Compute answers to 3 decimal places.

13. $y_1 = x + 2$ and $y_2 = 0$ on the interval $- 1\le{x}\le 5$

    $\begin{align}&\int_{-1}^5\left(\left(x+2\right)-0\right)\operatorname dx\end{align}$

    $\left(\frac{x^2}2+2x\right)│_{-1}^{5}$

    $(\frac{25}{2}+10)-(\frac{1}{2}-2)$

    $22.5+1.5$

    $24\ unit{{s}^{2}}$

14. $y_1 = {x^2} + 2x - 1$ and $y_2 = 0$ on the interval $ - 2 \le x \le 0$

    $\begin{align}& \int_{-2}^0\left(y_2-y_1\right)\operatorname dx\end{align}$

    $\begin{align}&\int_{-2}^{0}{0-({{x}^{2}}+2x-1)dx}\end{align}$

    $\begin{align}&\int_{-2}^{0}{-{{x}^{2}}-2x+1\ dx}\end{align}$

    $\left(\frac{-x^3}3-\frac{2x^2}2+x\right)│_{-2}^{0}$

    $\left(\frac{-x^3}3-x^2+x\right)│_{-2}^{0}$

    $0-(\frac{8}{3}-4-2)$

    $\frac{10}{3}\ unit{{s}^{2}}$

15. $y_1 = - {x^2} + 4x + 2$ and $y_2 = x$ on the interval $\frac{1}{2} \le x \le 3$

    $\begin{align}& \int_\frac12^3\left(y_2-y_1\right)\operatorname dx\end{align}$

    $\begin{align}&\int_\frac12^3(-{{x}^{2}}+4x+2)-x\ dx\end{align}$

    $\begin{align}&\int_\frac12^3\left(-{{x}^{2}}+3x+2\right)\ dx\end{align}$

    $\left(\frac{-x^3}3+\frac{3x^2}2+2x\right)│_\frac12^3$

    $(-9+\frac{27}{2}+6)-(\frac{-1}{24}+\frac{3}{8}+1)$

    $10.5-\frac{4}{3}$

    $9.17\ unit{{s}^{2}}$

16. $y_1 = \frac{1}{x}$ and $y_2 = {e^x}$ on the interval $1 \le x \le 2$

    $\begin{align}& \int_1^2\left(y_2-y_1\right)\operatorname dx\end{align}$

    $\begin{align}&\int_{1}^{2}{{{e}^{x}}-\frac{1}{x}\ }dx\end{align}$

    $({{e}^{x}}-\ln \left| x \right|)│_{1}^{2}$

    $({{e}^{2}}-\ln 2)-({{e}^{1}}-\ln 1)$

    $6.6959-2.71828$

    $3.98\ unit{{s}^{2}}$

17. $y_1 = {x^3} - 3x$ and $y_2 = x$

    $\begin{align}& \int_{-2}^0\left(y_1-y_2\right)\operatorname dx + \int_0^2\left(y_2-y_1\right)\operatorname dx\end{align}$

    $\begin{align}&\int_{-2}^0\left(\left(x^3-3x\right)-x\right)\ dx+\int_0^2\left(x-\left(x^3-3x\right)\right)\ dx\end{align}$

    $\begin{align}&\int_{-2}^0\left(x^3-4x\right)\ dx+\int_0^2\left(-x^3+4x\right)\ dx\end{align}$

    $\left(\frac{x^4}4-2x^2\right)│_{-2}^{0}+\left(\frac{-x^4}4+2x^2\right)│_{0}^{2}$

    $(0-0)-(4-8)+(-4+8)-(0+0)$

    $4+4$

    $8\ unit{{s}^{2}}$

18. The revenue from a manufacturing process is projected to follow the model $R'(x) = 150$ million per year for 10 years. The cost is projected to follow the model $C'(x) = 80 + 0.25{x^2}$ millions of dollars per year over the same period of time, where x is time in years.

    Approximate the profit over the 10-year period.

    $\begin{align}&P(x)=\int\left[R'(x)-C'(x)\right]\;dx\end{align} $

    $P(x)=\begin{align}&\int_{0}^{10}{150-(80+0.25{{x}^{2}}})dx\end{align} $

    $=\begin{align}&\int_{0}^{10}{70-0.25{{x}^{2}}dx}\end{align} $

    $=\left(70x-\frac{0.25x^3}3\right)│ _{0}^{10}$

    $=(70\cdot10-\frac{0.25{{\left( 10 \right)}^{3}}}{3})-(0-0) $

    The total profit will be $\$616.6$ million over the 10-year period.

19. Consider the functions given by $f(x) = - {x^2} + 2x + 4$ and $g(x) = 4 - x.$

    1. Use algebra to find the points where the graphs of f and g intersect.
    2. Sketch an accurate graph of f and g on the axes provided, labeling the curves by name and the intersection points with ordered pairs.
    3. What is the exact area between f and g between their intersection points?

    $\begin{align}&\int_0^3\left[f(x)-g(x)\right]\operatorname dx\end{align}$

    $\begin{align}&\int_0^3\left[\left(-x^2+2x+4\right)-\left(4-x\right)\right]dx\end{align}$

    $\begin{align}&\int_0^3\left(-x^2+2x+4-4+x\right)\ dx\end{align}$

    $\begin{align}&\int_0^3\left(-x^2+3x\right)\ dx\end{align}$

    $\left(\frac{-x^3}3+\frac{3x^2}2\right)│_0^3 $

    $4.5-0 $

    $4.5\ unit{{s}^{2}} $

20. Find the area of the region bounded by $y_1 = \sqrt x $ and $y_2 = \frac{1}{4}x$ .

    $y_1=\sqrt{x}$

    $y_2=\frac{1}{4}x$

    $\begin{align}&\int_0^{16}\left(y_1-y_2\right)\operatorname dx\end{align}$

    $\begin{align}&\int_0^{16}\left(\sqrt{x}-\frac14x\right)\ dx\end{align}$

    $\begin{align}&\int_{0}^{16}\left(x^\frac12-\frac14x\right)\ dx\end{align}$

    $\left(\frac{x^{\frac32}}{\frac32}-\frac14\cdot\frac{x^2}2\right)\vert_0^{16}$

    $\left(\frac23x^\frac32-\frac18x^2\right)│_0^{16}$

    $(\frac{2}{3}\cdot{{16}^{\frac{3}{2}}}-\frac{1}{8}\cdot{{16}^{2}})-(0-0)$

    $10.67\ unit{{s}^{{2}}}$

21. Find the area of the region bounded by $y_1 = 12 - 2{x^2}$ and $y_2 = {x^2} - 8$ .

    $y_1=12-2{{x}^{2}}$

    $y_2={{x}^{2}}-8$

    $\begin{align}&\int_{-2.58}^{2.58}\left[(12-2{{x}^{2}})-({{x}^{2}}-8)\right]dx\end{align}$

    $\begin{align}&\int_{-2.58}^{2.58}\left(12-2{{x}^{2}}-{{x}^{2}}+8\right) dx\end{align}$

    $\begin{align}&\int_{-2.58}^{2.58}\left(-3{{x}^{2}}+20\right)dx\end{align}$

    $\left(\frac{-3x^3}3+20x\right)│_{-2.58}^{2.58}$

    $(-x^3+20x)│_{-2.58}^{2.58}$

    $34.426-(-34.426)$

    $68.85\ unit{{s}^{2}}$

22. Find the area of the region bounded by the curves $y_1 = {x^3} - x$ and $y_2 = {x^2}.$

    $y_1={{x}^{3}}-x$

    $y_2={{x}^{2}}$

    $y_1$ and $y_2$ intersect at $x=-0.62$ and $x=1.62.$

    $\begin{align}&\int_{-0.62}^0\left(y_1-y_2\right)\operatorname dx\;+\int_0^{1.62}\left(y_2-y_1\right)\operatorname dx\end{align}$

    $\begin{align}&\int_{-0.62}^{0}\left[\left(x^3-x\right)-x^2\right]dx+\int_{0}^{1.62}\left[x^2-\left(x^3-x\right)\right]dx\end{align}$

    $\begin{align}&\int_{-0.62}^0\left(x^3-x^2-x\right)\;dx+\int_0^{1.62}\left(-x^3+x^2+x\right)\;dx\end{align}$

    $\left(\frac{x^4}4-\frac{x^3}3-\frac{x^2}2\right)│_{-0.62}^0 +\left(-\frac{x^4}4+\frac{x^3}3+\frac{x^2}2\right)│_0^{1.62}$

    $(0-(-0.0758))+(1.0075-0)$

    $0.0758+1.0075$

    $1.0833\ unit{{s}^{2}}$

    Source: Active Calculus by Matthew Boelkins is licensed under a Creative Commons Attribution-NonCommercial-ShareAlike 4.0 International License. Based on a work at http://scholarworks.gvsu.edu/books/10/.

23. The rate of change of the value of goods exported from the United States between 2000 and 2014 can be modeled as $$E'(t) = - 2688.96x{}^2 + 43524x - 35103.48$$ billion dollars per year $t$ years after the end of 2000.The rate of change of the value of goods imported into the United States between 2000 and 2014 can be modeled as $$I'(t) = 4485.04x + 144,264.16$$ billion dollars per year $t$ years after the end of 2000.

    Source: U.S. Census Bureau, Economic Indicator Division

    Find the difference in the accumulated value of imports and exports from 2000-2014.

    $\begin{align}&\int_0^{14}\left[I'\left(t\right)-E'\left(t\right)\right]\;\operatorname dt\end{align}$

    $\begin{align}&\int_{0}^{14}{(4485.04x+144264.16)-(-2688.96{{x}^{2}}+43524x-35103.48)dx}\end{align}$

    $\begin{align}&\int_{0}^{14}{4485.04x+144264.16+2688.96{{x}^{2}}-43524x+35103.48 dx}\end{align}$

    $\begin{align}&\int_{0}^{14}{2688.96{{x}^{2}}-39038.96x+179367.64 dx}\end{align}$

    $\left(\frac{2688.96x^3}3-\frac{39038.96x^2}2+179367.64x\right)│_0^{14}$

    $(896.32x^3-19519.48x^2+179367.64x)│_0^{14}$

    $1144830.96-0$

    $1144830.99$

    The imports exceeded exports by $\$1,144,830.96$ billion between 2000 and 2014.