MATH 1830
Unit 2 Applications of Derivatives
2.4 Graph Analysis: Polynomials
2.4 Video
Matching functions with their derivatives.
Match the function with its first and second derivatives.
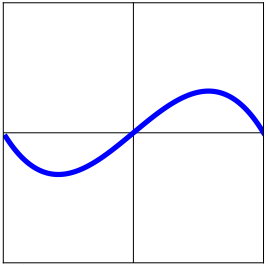
- Pick the graph of the First Derivative of the function above.
- Pick the graph of the Second Derivative of the function above.
- Match the function with its first and second derivatives.
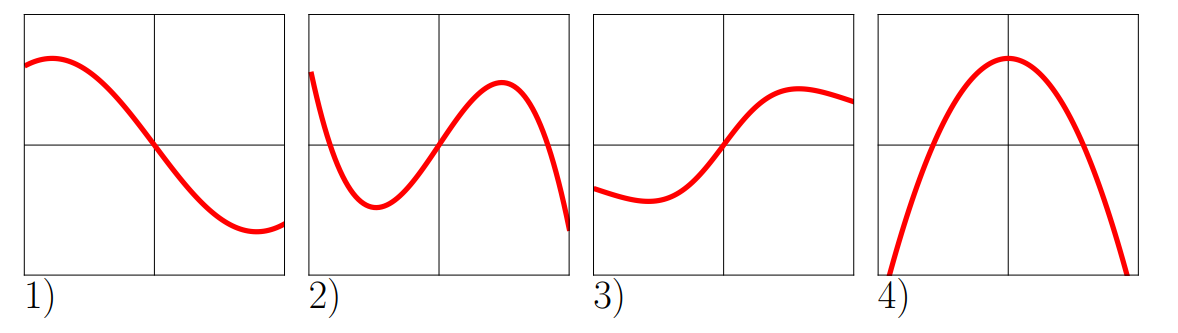
Graph 4
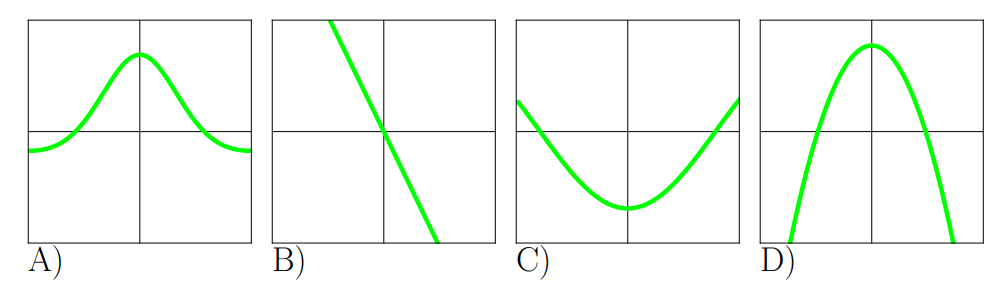
Graph B
Source Oliver Knill, Knill@math.harvard.edu, Math 1A, Harvard College, Spring 2020
2.4 Lecture
First Derivatives of the function above.

Second Derivatives of the function above.

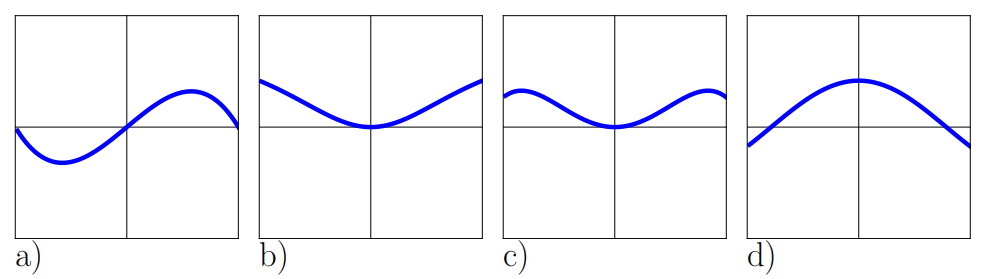
a,4,B
b,3,A
c,2,D
d,1,C
Source Oliver Knill, Knill@math.harvard.edu, Math 1A, Harvard College, Spring 2020