MATH 1830 Notes

Unit 2 Applications of Derivatives

2.6 Introduction to Optimization

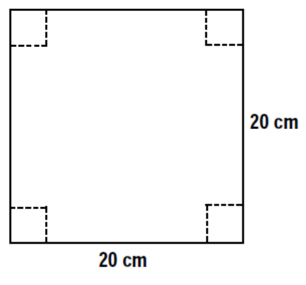
  1. Construct a 20 cm by 20 cm square on the white piece of paper.

  2. Draw four congruent squares in each corner of your original square (see diagram below), the size of the four squares you draw will be assigned for your group.

  3. Using the scissors and tape, cut out your square and its corners to create an open-topped box.

    20 cm by 20 cm Square with small squares made with dotted lines in each corner

  4. Complete the following questions:

    1. The width of our box is:
    2. The length of our box is:
    3. The height of our box is:
    4. Calculate the volume of your box.

    A summary of the data collected from the class is on the board. Copy this data into the chart below.

    Height (cm) Volume (cubic cm)
    0 0
    1
    2
    3
    4
    5
    6
    7
    8
    9
    10 0

  5. Using the graph paper, construct a graph of height vs volume by plotting the above ordered pairs. Join the points with a smooth curve. Answer the following questions based on your graph.

    1st Quadrant Graph with height on the x-axis and volume on the y-axis

    Blank 20 by 20 coordinate plane 

  6. What is the maximum volume? (According to your graph.)

  7. What size of square cut out of the corner would result in the maximum volume?

  8. What type of function models your graph?

  9. Could we write a mathematical function representing the graph?

  10. How could our knowledge of derivatives be used to find the maximum volume?