MATH 1830

Unit 2 Application of Derivatives

2.1 Marginal Analysis in Business and Economics



2.1 Video

Marginal Cost, Revenue and Profit

  1. A company’s market research department recommends the manufacture and marketing of a new 3 meter lightening-to-USB power cord. After suitable test marketing, the research department presents the following price demand equation: $$p = 12 - 0.001x$$ where x is demand at price p. The financial department provides the cost function that includes a fixed cost of \$5600 (tooling and overhead) and variable costs of \$1.80 per power cord (materials, labor, marketing, transportation, storage): $$C\left( x \right) = 5600 + 1.80x$$

    1. Marginal Cost Function: Find and interpret the Marginal Cost Function

      $C'(x) = 1.80$

      At any production level, the cost to produce one more power cord is \$1.80.

    2. Revenue Function: Find the Revenue Function as a function of x.

      Revenue is price multiplied by production level

      $R(x) = px = \left( {12 - 0.001x} \right)x$

      $R(x)=12x - 0.001{x^2}$

    3. Marginal Revenue Function: Find the Marginal Revenue function and find the marginal revenue at x = 2000, x = 5000, and x = 7000. Interpret the results.

      $R'\left( x \right) = 12 - 0.002x$

      $R'\left( {2000} \right) = 12 - 0.002\left( {2000} \right) = 8$

      Revenue increases by \$8 for the 2001st cord produced and sold.

      $R'\left( {5000} \right) = 2$

      Revenue increases by \$2 for the 5001st cord produced and sold.

      $R'\left( {7000} \right) = - 2$

      Revenue decreases by \$2 for the 7001st cord produced and sold.



    2. 2.1 Lecture


  2. From #1 the cost function is $C\left( x \right) = 5600 + 1.80x$ and the revenue function is $R(x)=12x - 0.001{x^2}$.
    1. Graph the cost function and the revenue function in the same coordinate system. Find the intersection points of these two graphs and interpret the results.

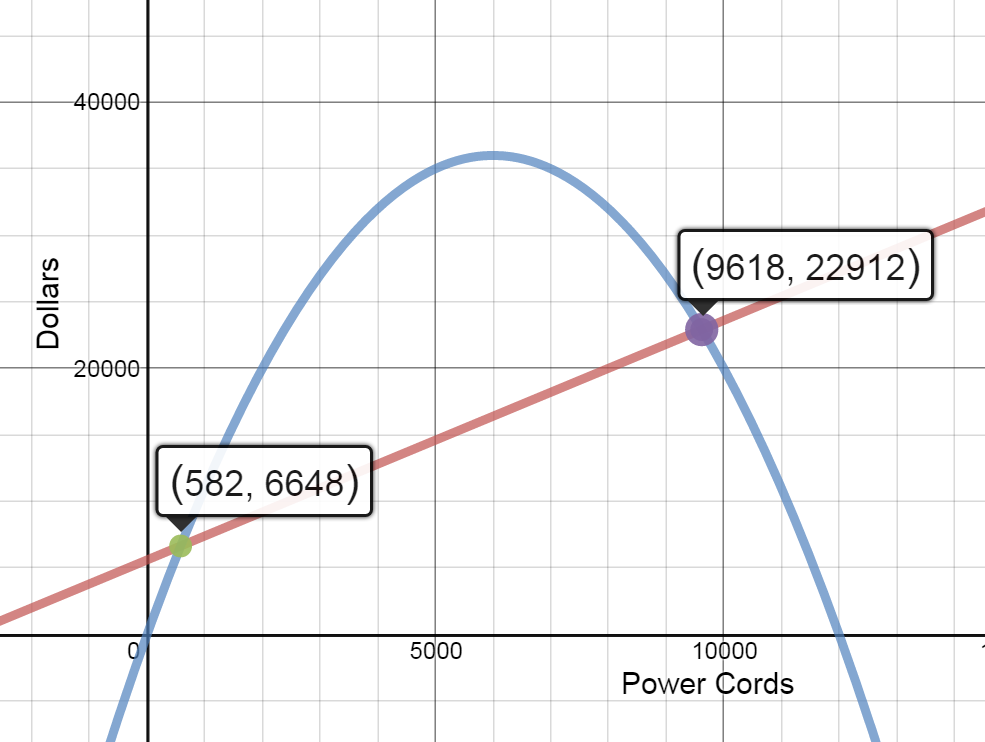
      x-axis: 0 to 12,000 in intervals of 2000, y-axis: 0 to 40,000 in intervals for 10,000. Linear cost function starts at the point (0, 5600) and rises to the right with a slope of 1.8. Quadratic revenue function has x-intercepts at (0,0) and (12000,0) with the vertex at (6000, 36000)

      At any production level between 0 and 582 power cords, revenue is less than cost. Therefore profit is negative.

      At any production level between 582 and 9618 power cords, revenue is greater than cost. Therefore profit is positive.

      At any production level great than 9618 power cords, revenue is less than cost. Therefore profit is negative.

    2. Profit Function: Find the profit function. Sketch the graph.

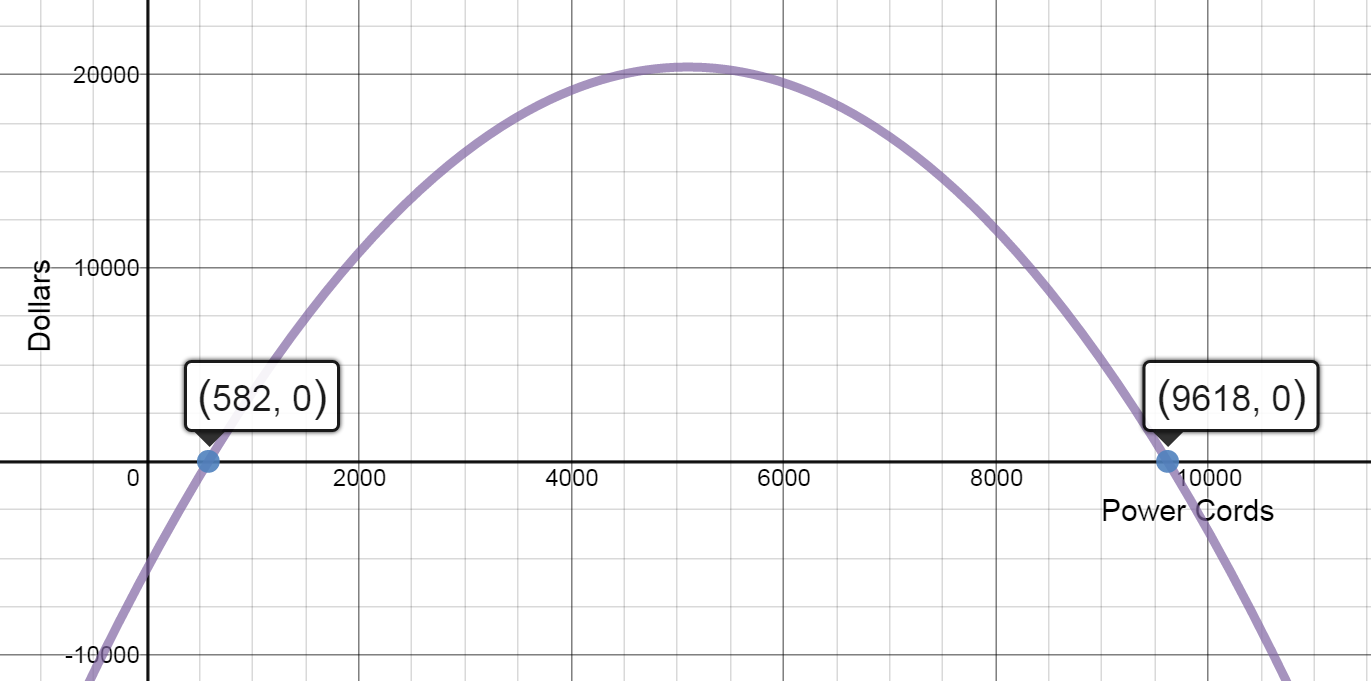
      Quadratic profit function -0.001x^2+10.2x-5600. x-axis: 0 to 10000 in intervals of 2000. y-axis: 0 to 20000 in intervals of 10000

      $P(x) = R(x) - C(x) = (12x - 0.001{x^2}) - (5600 + 1.8x) = $

      $P(x)=- 0.001{x^2} + 10.2x - 5600$

    3. Marginal Profit Function: Find the marginal profit function and evaluate the marginal profit at x = 1000, x = 4000, and x = 6000. Interpret the results.

      $P'\left( x \right) = - 0.002x + 10.2$

      $P'(1000) = - 0.002(1000) + 10.2 = 8.2$

      Profit increases by \$8.20 for the 1001st cord.

      $P'(4000) = - 0.002(4000) + 10.2 = 2.2$

      Profit increases by \$2.20 for 4001st cord.

      $P'(6000) = - 0.002(6000) + 10.2 = - 1.8$

      Profit decreases by \$1.80 for 6001st cord.



    2.1 Group Work


  3. A new streaming service has concluded that the demand for their service follows $p=250-0.05x$ where $p$ is the yearly price in dollars and $x$ is the number of subscribers in thousands.

    1. Find $R(x)$

      $R(x) = x \cdot p$

      $R(x)=x(250-0.05x)$

      $R(x)=250x-0.05x^2$

    2. Find the number of subscribers when $p=150$

      $250-0.05x=150$

      $100=0.05x$

      $x=2000$   There would be 2,000,000 subscribers

    3. Rind the total revenue when $p=150$

      $R(2000)=250(2000)-0.05(2000)^2$

      $R(2000)=300,000$  The total revenue would be $300,000

  4. A shop manufactures performance bikes. The manager estimates that the total cost (in dollars) of producing b bikes is: $$C\left( b \right) = 1200 + 25b - 0.14{b^2}$$

    1. Average Cost: Find the average cost function, $\bar C\left( b \right)$. Calculate $\bar C\left( 7 \right)$ and interpret the results.

      $\bar C\left( b \right)\, = \frac{{1200 + 25b - 0.14{b^2}}}{b}$

      $\bar C\left( b \right)\, = \frac{{1200}}{b} + 25 - 0.14b$

      $\bar C\left( 7 \right)\, = \frac{{1200}}{7} + 25 - 0.14(7) = 195.45$

      The average cost of producing 7 bikes is \$195.45.

    2. Marginal Cost: Find the Marginal Cost Function,$ C'\left( b \right)$. Calculate $ {C'} \left( 7 \right)$ and interpret the results.

      $ C\left( b \right)\, = 1200 + 25b - 0.14{b^2}$

      ${C ^\prime }\left( b \right) = 25-0.28b$

      ${ C ^\prime }\left( 7 \right) = 23.04$

      When the 8th bike is produced, the marginal cost is \$23.04.

    3. Explain the difference between parts a and b.

      On average, the cost to produce each of the 7 bikes is \$195.45. The cost to produce the 8th bike is approximately \$23.04.

    5.  

    2.1 Additional Practice

  5. You are the manager of Sassy Surf Creations, a new trend-setting clothing manufacturer. The cost function for your very exclusive Tai Kwon Do Dragon T-shirts is $$C\left( x \right)=0.02{{x}^{2}}+7.5x+600$$ in dollars, and you sell the shirts for $\$20.00$ each. Determine the following.

    1. The revenue function

      $R(x)=20.00x$



    2. The marginal revenue function

      ${R}'\left( x \right)=20.00$



    3. The profit function

      $P(x)=R(x)-C(x)$

      $P(x)=20.00x-\left( 0.02{{x}^{2}}+7.50x+600 \right)$

      $P(x)=20.00x-0.02{{x}^{2}}-7.50x-600$

      $P(x)=-0.02{{x}^{2}}+12.50x-600$



    4. The marginal profit function

      $P'\left( x \right)=-0.04x+12.50$



    5. The marginal revenue and marginal profit for the sale of 300 T-shirts

      ${R}'\left( 300 \right)=\$20.00$

      ${P}'\left(300\right)=-0.04\left(300\right)+12.50=\$0.50$



    6. Explain what marginal revenue and profit mean, in general.

      At a specific production level, the revenue and profit generated if one more is produced and sold.



    7. Explain what the marginal revenue and marginal profit mean for the sale of 300 T-shirts.

      The revenue for the 301st T-shirt is \$$20.00$. The profit for the 301st T-shirt is \$$0.50.$

  6. The total cost, in dollars, of operating a factory that produces gourmet gas ranges is $$C(x)=0.5{{x}^{2}}+40x+8000,$$ where x is the number of gas ranges produced.

    1. Determine the marginal cost of producing 5000 gas ranges and compare this with the actual cost of producing the 5001st gas range.

      ${C}'\left( x \right)=x+40$

      ${C}'\left( 5000 \right)=5000+40=\$5040$ Estimated cost to produce 5001st gas range

      The actual cost to produce the 5001st gas range is $C\left( 5001 \right)-C\left( 5000 \right).$

      $C(5001)=\$12,713,040.50$

      $C(5000)=\$12,708,000.00$

      $C\left( 5001 \right)-C\left( 5000 \right)=5040.50$

      Actual cost to produce 5001st gas range is \$$5040.50.$



    2. Determine the average cost of producing 5000 gas ranges. Compare this value to those in part a. What do you notice?

      $\overline{C}(x)=\frac{0.5{{x}^{2}}+40x+8000}{x}=0.5x+40+\frac{8000}{x}$

      $\overline{C}(5000)=0.5(5000)+40+\frac{8000}{5000}=\$2541.60$

      The average cost is significantly less than the cost of producing the 5001st gas range.

  7. The cost, in dollars, of producing x hot tubs is modeled by $C(x)=3450x-1.02{{x}^{2}},$ when the company produces up to 1500 hot tubs.

    ${C}'\left( x \right)=3450-2.04x$

    1. Determine the marginal cost when 750 hot tubs are made. What does this mean to the manufacturer?

      ${C}'(750)=3450-2.04(750)=\$1920$

      The estimated cost to produce the 751st hot tub is \$1920.



    2. Find the cost of producing the 751st hot tub.

      $C(751)-C(750)=2015668.98-2013750 =\$1918.98$

      The actual cost to produce the 751st hot tub is \$1918.98.



    3. Compare and comment on the values in parts a and b.

      Marginal cost (a) is an approximation for the cost of the next item. The actual cost (b) is the exact cost according to the model (not an approximation).



    4. Each hot tub is sold for $9200. Write a revenue function for the sale of x hot tubs.

      $R(x)=9200x$



    5. Determine the rate of change of the profit for the sale of 750 hot tubs.

      $P(x)=R(x)-C(x)=9200x-(3450x-1.02{{x}^{2}})$

      $P(x) =1.02{{x}^{2}}+5750x$

      $P'(x)=2.04x+5750$

      $P'(750)=2.04(750)+5750=\$7280$

      Profit is increasing by \$7280 for each hot tub, when 750 are produced.

  8. The National Honor Society at a local high school sells T-shirts for its yearly fundraiser. The cost of producing the x shirts is $$C(x)=-0.0005{{x}^{2}}+7.5x+200,$$ and each shirt sells for \$$15.00$.

    1. Determine the revenue function.

      $R(x)=15x$



    2. Determine the marginal cost function.

      $C'(x)=-0.0010x+7.5$



    3. Determine the marginal revenue function.

      $R'(x)=\$15$

      Revenue increases by \$15 for each T-shirt sold.



    4. Determine the marginal cost AND the marginal revenue when 1500 shirts are sold.

      $C'(1500)=-0.0010\left( 1500 \right)+7.5=\$6$

      The cost to produce the 1501st shirt is \$6.

      ${R}'\left(1500\right)=\$15$

      The revenue for the 1501st shirt is \$15.



    5. Determine the ACTUAL cost of producing the 1501st shirt, according to the model.

      $C( 1501)-C( 1500)$

      $=\left( -0.0005{{(1501)}^{2}}+7.5(1501)+200 \right)-\left( -0.0005{{(1500)}^{2}}+7.5(1500)+200 \right)$

      $= 10330.995-10325=10330.995-10325=5.995$

      The actual cost to produce the 1501st shirt is $\$5.995.$



    6. Determine the profit and the marginal profit from the sale of 1500 shirts.

      $P(x)=R(x)-C(x)=15x-\left( -0.005{{x}^{2}}+7.5x+200 \right)$

      $P(x)=0.0005{{x}^{2}}+7.5x-200$

      ${P}'(x)=0.001x+7.5$

      $P\left( 1500 \right)=\$12,175$

      ${P}'\left( 1500 \right)=\$9$

      The profit from the sale of 1500 shirts is \$12,175. The profit would be increased by \$9.00 if one more shirt is sold (1501 shirts sold).