MATH 1830 Notes

Unit 3 Derivative Rules

3.6 Graph Analysis: Rational Functions


First Derivative Test

Analyze $f'(x)$ to Identify Intervals of Increase/Decrease and Extrema on the Graph of $f(x).$

  1. Find $f'(x)$
  2. Identify all critical numbers and partitions for the function.
    1. Values of $x$ where$f'(x)=0$ are critical numbers.
    2. Values of $x$ where $f'(x)$ is undefined are partitions.
    3. Values of $x$ where $f(x)$ is undefined are partitions.
  3. Graph the critical numbers and partitions on a number line, separating the number line into intervals.
  4. Determine the intervals on which $f(x)$ is increasing /decreasing
    1. Test one point contained in the interval (do not use the end points of the interval).
    2. $f'(x)<0$ then the function $f(x)$ is DECREASING on the interval
    3. $f'(x)>0$ then the function $f(x)$ is INCREASING on the interval
  5. Identify local maxima and minima of $f(x)$ using the First Derivative Test.
    1. On the interval $(a,c)$, a local maximum occurs at $f(b)$ when $f(x)$ is increasing for all $x$ in the interval $(a,b]$ and $f(x)$ is decreasing for all $x$ in the interval $[b,c)$.
    2. On the interval $(a,c)$, a local minimum occurs at $f(b)$ when $f(x)$ is decreasing for all $x$ in the interval $(a,b]$ and $f(x)$ is increasing for all $x$ in the interval $[b,c)$.

Second Derivative Test

Analyze $f''(x)$ to Identify Intervals of Concavity and Points of Inflection on the Graph of $f(x).$

  1. Find $f''(x).$
  2. Find the critical numbers for the function.
    1. Values of $x$ where $f''(x)=0$ are critical numbers.
    2. Values of $x$ where $f''(x)$ is undefined are partitions.
    3. Values of $x$ where $f(x)$ is undefined are partitions.
  3. Graph the critical numbers and partitions on a number line, separating the number line into intervals.
  4. Determine the intervals on which $f(x)$ is concave up or concave down.
    1. Test one point contained in the interval (do not use the end points of the interval).
    2. $f(x)$ is concave down on the interval if $f''(x)<0$.
    3. $f(x)$ is concave up on the interval if $f''(x)>0$.
  5. Identify inflection points of $f(x)$. A point of inflection occurs at $x=a$ when $f''(a)=0$ and $f''(x)$ changes concavity across $a$.

3.6 Video

Use the First & Second Derivative Tests to analyze the function. Identify x- & y-intercepts, any holes or asymptotes (if they exist), intervals of increase/decrease, extrema, interval of concavity, and inflection points on the graph of the function.

  1. $f(x)=\frac{3x+4}{2x-5}$

    1. Increasing and Decreasing

      ${f}'\left( x \right)=\frac{3\left( 2x-5 \right)-2\left( 3x+4 \right)}{{{\left( 2x-5 \right)}^{2}}}=\frac{6x-15-6x-8}{{{\left( 2x-5 \right)}^{2}}}=\frac{-23}{{{\left( 2x-5 \right)}^{2}}}$

      Values of x where ${f}'\left( x \right)=0:$

      $\frac{0}{1}=\frac{-23}{{{\left( 2x-5 \right)}^{2}}}$

      $-23 \neq 0$. There are no values of x where ${f}'\left( x \right)=0.$

      Values of x where ${f}'\left( x \right)$ is undefined:

      $2x-5=0$, $ x=\frac{5}{2}$

      Values of x where $f\left( x \right)$ is undefined:

      $2x-5=0$, $x=\frac{5}{2}$

      Separate into intervals using: $x=\frac{5}{2}$.

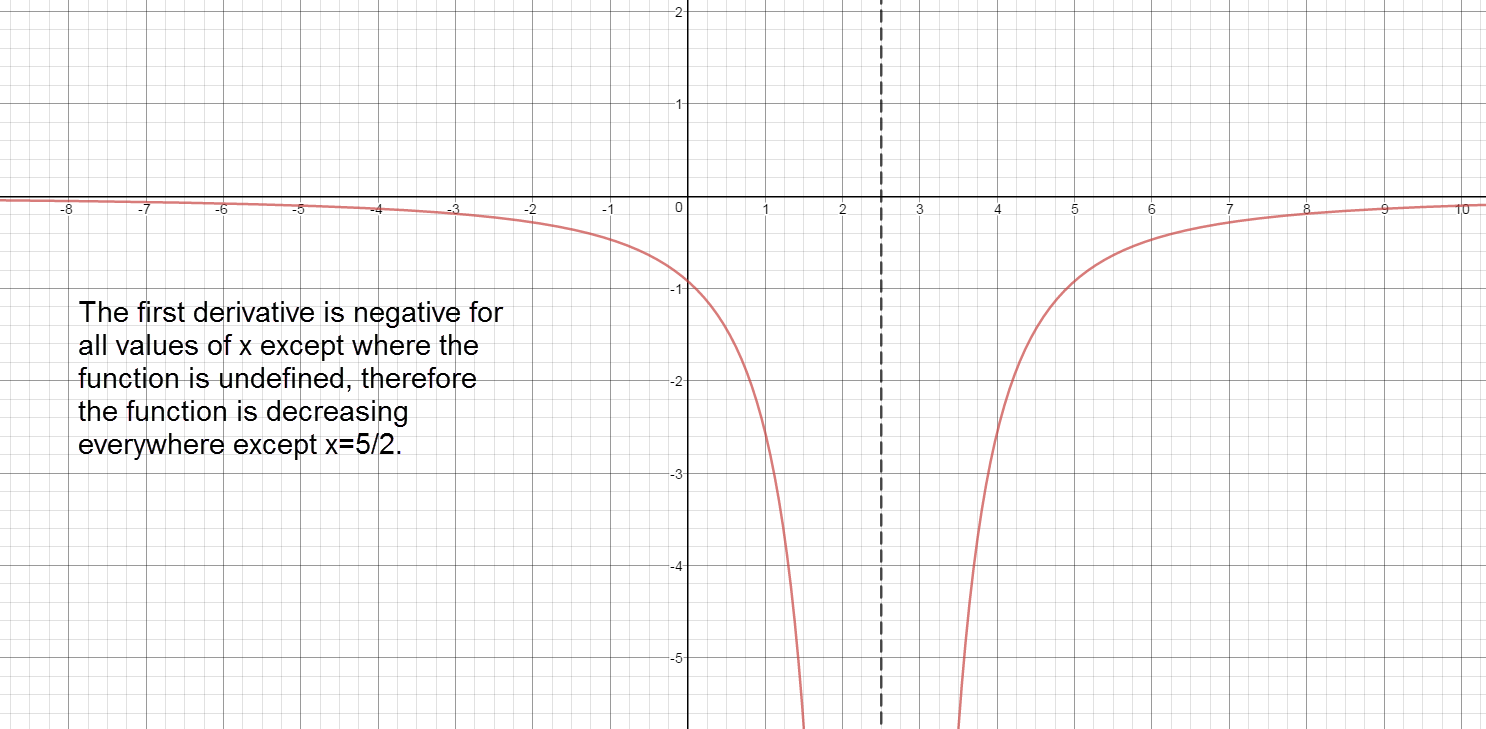
      Image of graph of F prime of x as it relates to the x axis. Separates graph into intervals divided by partitions where F prime equals zero, or is undefined. Also indicates intervals where derivative is positive and intervals where derivative is negative.
      Sign graph of ${f}'(x)$ reading left to right: negative, ${f}'\left( \frac{5}{2} \right)\text{= undefined}$, negative

      Increasing:

      The graph of the first derivative is never above the x axis. Therfore, there are no intervals where $f(x)$ is increasing.

      Decreasing:

      $\left( -\infty ,\frac{5}{2} \right)\cup \left( \frac{5}{2},\infty \right)$ The graph of the first derivative is always below the x axis. Therefore, the function is decreasing over the entire domain.

    2. Local Maxima:

      The first derivative never changes from positive to negative. There are no local maxima.

      Local Minima:

      The first derivative never changes from negative to positive. There are no local minima.

    3. Concave Up and Concave Down

      ${f}''\left( x \right)=-23\left( -2 \right){{\left( 2x-5 \right)}^{-3}}\left( 2 \right)=\frac{92}{{{\left( 2x-5 \right)}^{3}}}$

      Values of x where ${f}''(x)=0$:

      There are no values of x where ${f}''\left( x \right)=0$.

      Values of x where ${f}''\left( x \right)$ is undefined:

      $ 2x-5=0$

      $ x=\frac{5}{2}$

      Values of x where $f\left( x \right)$is undefined:

      $2x-5=0$

      $x=\frac{5}{2}$

      Separate into intervals using: $x=\frac{5}{2}$.

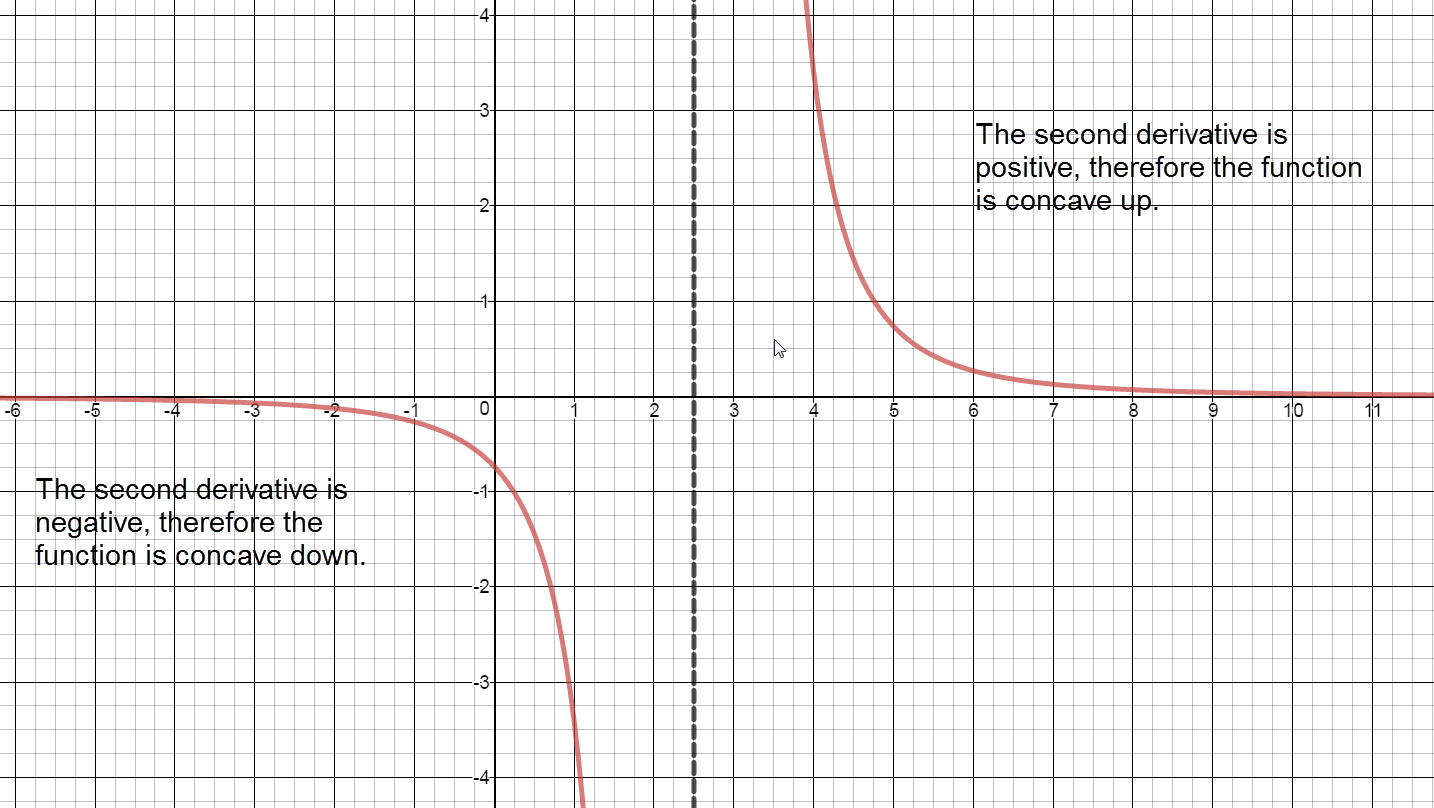
      Graph of Second Derivative of f of x and how it relates to the x axis. Intervals are separated by values of x where the second derivative equals 0 or is undefined. Values where f of x is undefined also serve to segment intervals. The graph indicates intervals where the second derivative of f of x is positive and where the second derivative is negative.
      Sign chart for ${f}''\left( x \right)$: negative, ${f}''\left( \frac{5}{2} \right)=$ undefined, positive

      Concave up:

      The graph of $f(x)$ is concave up on the interval $\left( \frac{5}{2},\infty \right).$

      Concave down:

      The graph of $f(x)$ is concave down on the interval $\left( -\infty ,\frac{5}{2} \right).$

    4. Inflection Points:

      Even though the function changes from concave down to concave up at $x=\frac{5}{2}$, there are no points of inflection because the function is undefined at $x=\frac{5}{2}.$

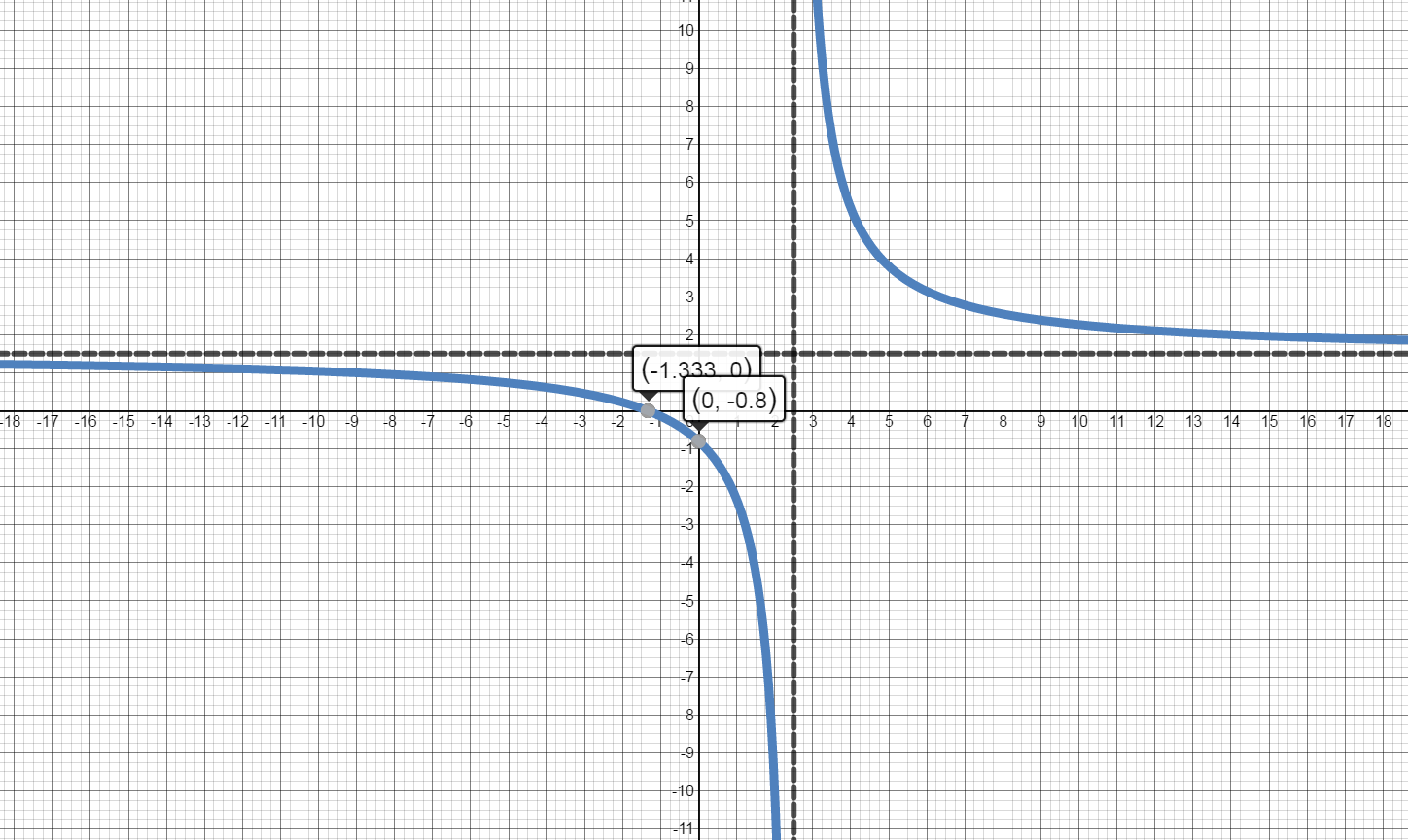
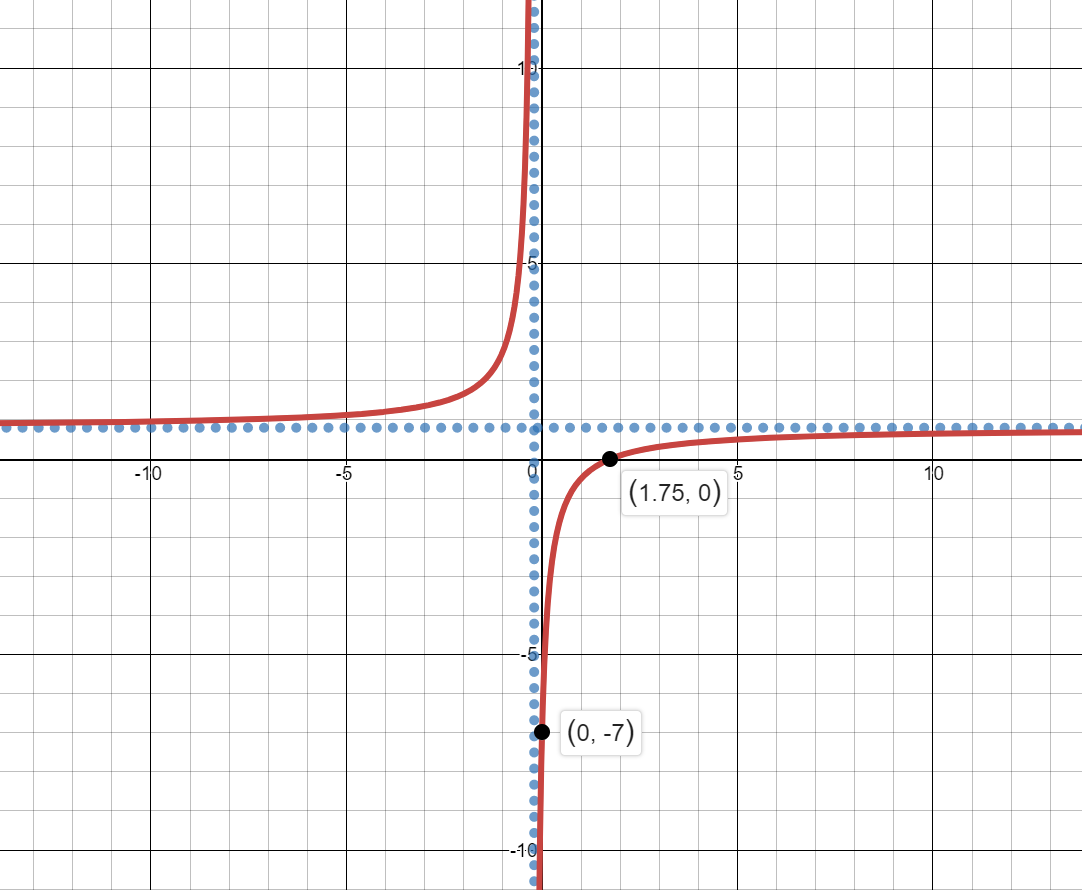
      Graph of f of x indicating intervals of increase, intervals of decrease, local maxima and local minima

    2. 3.6 Lecture

    Use the First & Second Derivative Tests to analyze the function. Identify x- & y-intercepts, any holes or asymptotes (if they exist), intervals of increase/decrease, extrema, interval of concavity, and inflection points on the graph of the function.

  2. $f(x)=\frac{4x-7}{5x+1}$

    1. Increasing and Decreasing

      ${f}'\left( x \right)=\frac{4\left( 5x+1 \right)-5\left( 4x-7 \right)}{{{\left( 5x+1 \right)}^{2}}}=\frac{20x+4-20x+35}{{{\left(5x+1 \right)}^{2}}}=\frac{39}{{{\left(5x+1 \right)}^{2}}}$

      Values of x where ${f}'\left( x \right)=0:$

      $\frac{0}{1}=\frac{39}{{{\left( 5x+1 \right)}^{2}}}$

      $39 \neq 0$. There are no values of x where ${f}'\left( x \right)=0.$

      Values of x where ${f}'\left( x \right)$ is undefined:

      $5x+1=0$, $ x=-\frac{1}{5}$

      Values of x where $f\left( x \right)$ is undefined:

      $5x+1=0$, $ x=-\frac{1}{5}$

      Separate into intervals using: $x=-\frac{1}{5}$.

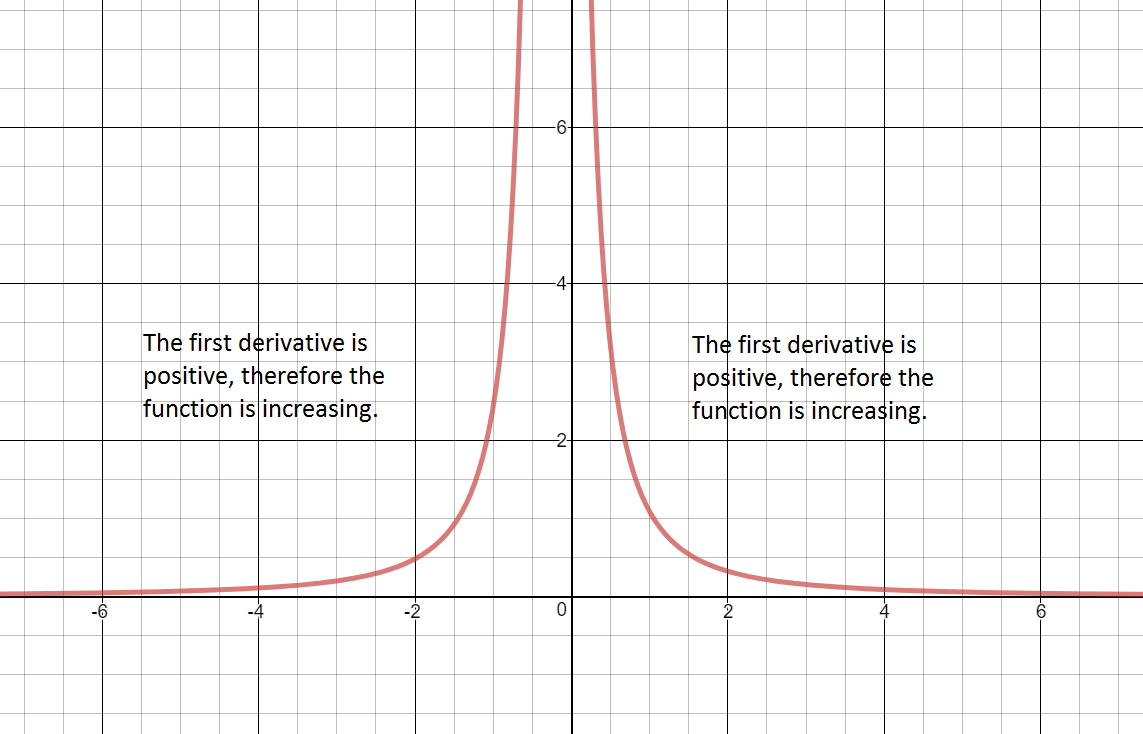
      Image of graph of F prime of x as it relates to the x axis. Separates graph into intervals divided by partitions where F prime equals zero, or is undefined. Also indicates intervals where derivative is positive and intervals where derivative is negative.
      Sign graph of ${f}'(x)$ reading left to right: positive, ${f}'\left( -\frac{1}{5} \right)\text{= undefined}$, positive

      Increasing:

      $\left( -\infty ,-\frac{1}{5} \right)\cup \left( -\frac{1}{5},\infty \right)$ The graph of the first derivative is always above the x axis. Therefore, the function is increasing over the entire domain.

      Decreasing:

      The graph of the first derivative is always above the x axis. Therfore, there are no intervals where $f(x)$ is decreasing.

    2. Local Maxima:

      The first derivative never changes from positive to negative. There are no local maxima.

      Local Minima:

      The first derivative never changes from negative to positive. There are no local minima.

    3. Concave Up and Concave Down

      ${f}''\left( x \right)=39\left( -2 \right){{\left( 5x+1 \right)}^{-3}}\left( 5 \right)=-\frac{390}{{{\left( 5x+1 \right)}^{3}}}$

      Values of x where ${f}''(x)=0$:

      There are no values of x where ${f}''\left( x \right)=0$.

      Values of x where ${f}''\left( x \right)$ is undefined:

      $ 5x+1=0$

      $ x=-\frac{1}{5}$

      Values of x where $f\left( x \right)$is undefined:

      $5x+1=0$

      $x=-\frac15$

      Separate into intervals using: $x=-\frac{1}{5}$.

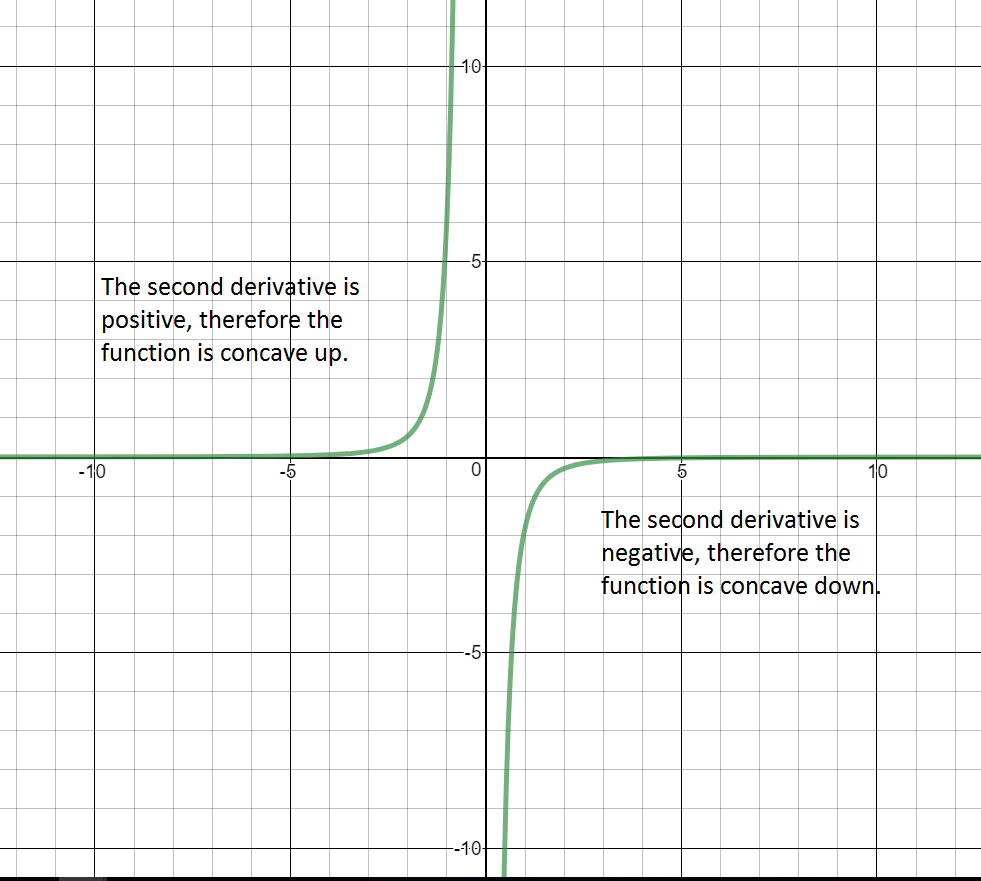
      Graph of Second Derivative of f of x and how it relates to the x axis. Intervals are separated by values of x where the second derivative equals 0 or is undefined. Values where f of x is undefined also serve to segment intervals. The graph indicates intervals where the second derivative of f of x is positive and where the second derivative is negative.
      Sign chart for ${f}''\left( x \right)$: positive, ${f}''\left( -\frac{1}{5} \right)=$ undefined, negative

      Concave up:

      The graph of $f(x)$ is concave up on the interval $\left( -\infty ,-\frac{1}{5} \right).$

      Concave down:

      The graph of $f(x)$ is concave down on the interval $\left( -\frac{1}{5},\infty \right).$

    4. Inflection Points:

      Even though the function changes from concave up to concave down at $x=-\frac{1}{5}$, there are no points of inflection because the function is undefined at $x=-\frac{1}{5}.$

      Graph of f of x indicating intervals of increase, intervals of decrease, local maxima and local minima

    3. 3.6 Group Work

    Use the First & Second Derivative Tests to analyze the function. Identify x- & y-intercepts, any holes or asymptotes (if they exist), intervals of increase/decrease, extrema, interval of concavity, and inflection points on the graph of the function.

  3. $f(x)=\frac{x^2+2x-8}{x+5}$

    1. Increasing and Decreasing

      ${f}'(x)=\frac{(2x+2)(x+5)-1(x^2+2x-8)}{(x+5)^2}=\frac{2x^2+10x+2x+10-x^2-2x+8}{(x+5)^2}=\frac{x^2+10x+18}{(x+5)^2}$

      Values of x where ${f}'\left( x \right)=0:$

      $\frac{0}{1}=\frac{x^2+10x+18}{(x+5)^2}$

      $x^2+10x+18=0$

      This will not factor so use Desmos.com

      $ {f}'(x)=0$ at $x=-7.646$ and $x=-2.354$

      Values of x where ${f}'(x)$ is undefined:

      $x+5=0$, $ x=-5$

      Values of x where $f(x)$ is undefined:

      $x+5=0$, $ x=-5$

      Separate number line into intervals using: $x=-7.646, -5, and -2.354$.

      Number line with critical values and partitions marked on the x-axis. Critical values are -7.646 and -2.354. the partition is at -5. Test values are also labeled on the number line: -8, -6, 0, and -3. There are arrows above the number line indicating where the graph is increasing and decreasing. The arrows are pointing up in the intervals from negative infinity to -7.646 and from -2.354 to infinity. The arrows are pointing down on the intervals from -7.646 to -5 and -5 to -2.354.

      Increasing:   $(-\infty,-7.646)$ U $(-2.354,\infty)$

      Decreasing:   $(-7.646, -5)$ U $(-5, -2.354)$

    2. Local Maxima:

      $(-7.646, -13.292)$

      Local Minima:

      $(-2.354, -2.708)$

    3. Concave Up and Concave Down

      ${f}''=\frac{(2x+10)(x+5)^2-2(x+5)(x^2+10x+18)}{(x+5)^4}$

      ${f}''=\frac{(2x+10)(x+5)-2(x^2+10x+18)}{(x+5)^3}$

      ${f}''=\frac{2x^2+10x+10x+50-2x^2-20x-36}{(x+5)^3}$

      ${f}''=\frac{14}{(x+5)^3}$

      Values of x where ${f}''(x)=0$:

      There are no values of x where ${f}''\left( x \right)=0$.

      Values of x where ${f}''(x)$ is undefined:

      $ x+5=0$

      $ x=-5$

      Values of x where $f\left( x \right)$is undefined:

      $x+5=0$

      $x=-5$

      Separate into intervals using: $x=-5$.

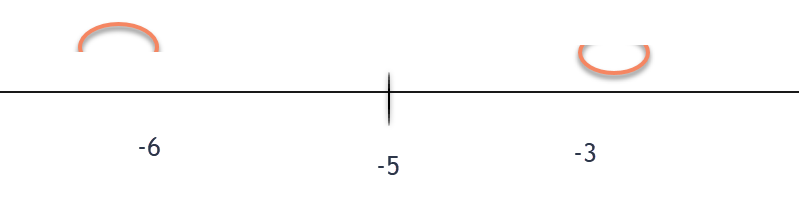
      Number line with the partition marked on the x-axis at -5. Test values are also labeled on the number line:-6 and -3. There are u's above the number line indicating where the graph is concave up and down. The concave up u is in the interval from negative infinity to -5 to infinity. The concave down u is on the interval-5 to infinity.

      The graph of $f(x)$ is concave up on the interval $( -5 , \infty).$

      Concave down:

      The graph of $f(x)$ is concave down on the interval $( -\infty, -5).$

    4. Inflection Points:

      Even though the function changes from concave up to concave down at $x=-5$, there are no points of inflection because the function is undefined at $x=-5.$

  4. Construct a sketch of the graph of a function of $f$ that has the given properties.
    1. $f(x)$   is such that
      • $f'(5)=0$
      • $f'(x)< 0$  on the interval $(-\infty,5)$
      • $f'(x)>0$  on the interval $(5,\infty)$
      • $f''(x)>0$  on the interval $(-\infty,\infty)$
      Blank coordinate plane graph with both the x- and y-axes going from -5 to 5.

      • $f(0)=2$
      • $f'(-3)=0$ and $f'(4)=0$
      • $f'(x)<0$   on the interval $(-3,4)$
      • $f'(x)>0$   on the intervals $(-\infty,-3)$   and   $(4,\infty)$
      • $f''(x)<0$  on the interval $(-\infty,0)$
      • $f''(x)>0$  on the interval $(0,\infty)$
      Blank coordinate plane graph with both the x- and y-axes going from -5 to 5.

      • $f(4)$ is undefined
      • $f'(4)$ is undefined
      • $f''(4)$ is undefined
      • $f(0)=0$
      • $f'(x)<0$   on the intervals $(-\infty,4)$   and   $(4,\infty)$
      • $f'(x)>0$ nowhere
      • $f''(x)<0$ on the interval $(-\infty,4)$
      • $f''(x)>0$ on the interval $(4, \infty)$

    5. 3.6 Additional Practice

    Use the First & Second Derivative Tests to analyze the function. Identify x- & y-intercepts, any holes or asymptotes (if they exist), intervals of increase/decrease, extrema, interval of concavity, and inflection points on the graph of the function.

  5. $f(x)=\sqrt[3]x-x$

    1. Increasing and Decreasing

      ${f}'(x)=\frac13x^\frac{-2}3-1=\frac1{3\sqrt[3]{x^2}}-1$

      Values of x where ${f}'\left( x \right)=0:$

      $\frac{0}{1}=\frac1{3\sqrt[3]{x^2}}-1$

      $\frac1{3\sqrt[3]{x^2}}=1$

      $3\sqrt[3]{x^2}=1$

      $\sqrt[3]{x^2}=\frac13$

      $x^2=\frac1{27}$

      $x=\pm\sqrt{\frac1{27}}$

      $ {f}'(x)=0$ at $x=-0.192$ and $x=0.192$

      Values of x where ${f}'(x)$ is undefined:

      $\sqrt[3]{x^2}=0$, $ x=0$

      Values of x where $f(x)$ is undefined:

      There is nowhere that $f(x)$  is undefined

      Separate number line into intervals using: $x=-0.192, x=0, x=0.192$.

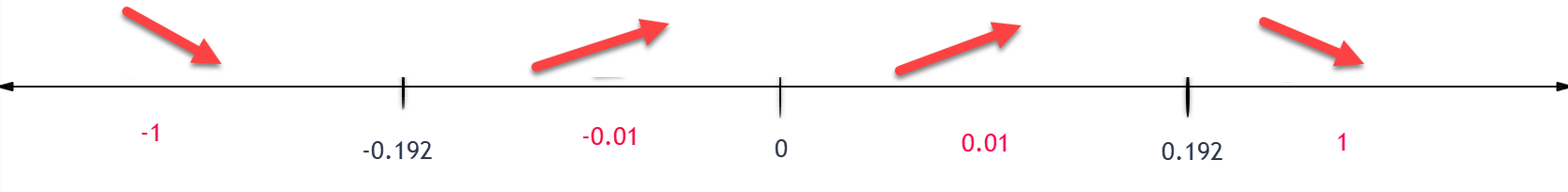
      Number line with critical values and partitions marked on the x-axis. Critical values are -0.192 and 0.192. the partition is at 0. Test values are also labeled on the number line: -1, -0.01, 0.01, and 1. There are arrows above the number line indicating where the graph is increasing and decreasing. The arrows are pointing Down in the intervals from negative infinity to -0.192 and from 0.192 to infinity. The arrows are pointing up on the intervals from -0.192 to 0 and 0 to 0.192.

      Increasing:   $(-0.192,0)$ U $(0,0.192)$

      Decreasing:   $(-\infty, -0.192)$ U $(0.192, \infty)$

    2. Local Maxima:

      $(0.192, 0.385)$

      Local Minima:

      $(-0.192, -0.385)$

    3. Concave Up and Concave Down

      ${f}''(x)=-\frac23\left(\frac13x^{\frac{-2}3-1}\right)=-\frac29x^\frac{-5}3$

      ${f}''(x)=-\frac2{9\sqrt[3]{x^5}}$

      Values of x where ${f}''(x)=0$:

      $-\frac2{9\sqrt[3]{x^5}}=\frac01$.

      $-2=0$.

      There are no critical values for ${f}''(x)$ .

      Values of x where ${f}''(x)$ is undefined:

      $\sqrt[3]{x^5}=0$

      $ x=0$

      Values of x where $f\left( x \right)$is undefined:

      There are no values of x where $f\left( x \right)$is undefined.

      Separate into intervals using: $x=0$.

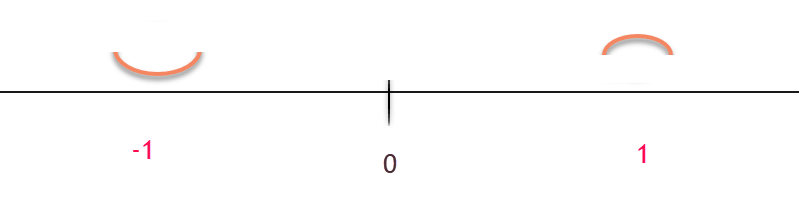
      Number line with the partition marked on the x-axis at 0. Test values are also labeled on the number line:-1 and 1. There are u's above the number line indicating where the graph is concave up and down. The concave up u is in the interval from negative infinity to 0 to infinity. The concave down u is on the interval0 to infinity.

      Concave up:

      The graph of $f(x)$ is concave up on the interval $( -\infty, 0).$

      Concave down:

      The graph of $f(x)$ is concave down on the interval $( 0 , \infty).$

    4. Inflection Points:

      Even though the function changes from concave up to concave down at $x=0$, there is no point of inflection because the second derivative is undefined at $x=0.$